dgeoutils 2.2.4 → 2.2.8

package/dist/DCircle.d.ts

@@ -3,10 +3,6 @@ import { DPolygon } from './DPolygon';
 export declare class DCircle {
     center: DPoint;
     r: number;
-    /**
-     * @param [center=(0,0)]
-     * @param [r=0]
-     */
     constructor(center?: DPoint, r?: number);
     toString(): string;
     getValue(): {
@@ -14,33 +10,9 @@ export declare class DCircle {
         r: number;
     };
     clone(): DCircle;
-    /**
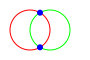
-     * Find intersection points with other circle.
-     *
-     * ![Example](https://edejin.github.io/DGeoUtils/media/examples/findPoints.png)
-     * @param c
-     */
     findPoints(c: DCircle): DPoint[] | number;
     equal({ center, r }: DCircle): boolean;
-    /**
-     * Transform circle to polygon
-     *
-     * ![Example](https://edejin.github.io/DGeoUtils/media/examples/findPolygonInside.png)
-     * @param [pointCount=64]
-     */
     findPolygonInside(pointCount?: number): DPolygon;
-    /**
-     * Transform circle to polygon on sphere. It would be different for different latitude.
-     *
-     * @remarks
-     * Center should be Lng/Lat.
-     *
-     * @remarks
-     * Radius should be in meters.
-     *
-     * ![Example](https://edejin.github.io/DGeoUtils/media/examples/findPolygonInsideOnSphere.png)
-     * @param [pointCount=64]
-     */
     findPolygonInsideOnSphere(pointCount?: number): DPolygon;
     private sphereOffset;
 }

package/dist/DCircle.js

@@ -5,13 +5,7 @@ const DPoint_1 = require("./DPoint");
 const DPolygon_1 = require("./DPolygon");
 const DNumbers_1 = require("./DNumbers");
 const utils_1 = require("./utils");
-// eslint-disable-next-line padded-blocks
 class DCircle {
-    /**
-     * @param [center=(0,0)]
-     * @param [r=0]
-     */
-    // eslint-disable-next-line no-useless-constructor,no-empty-function
     constructor(center = DPoint_1.DPoint.zero(), r = 0) {
         this.center = center;
         this.r = r;
@@ -25,12 +19,6 @@ class DCircle {
     clone() {
         return new DCircle(this.center, this.r);
     }
-    /**
-     * Find intersection points with other circle.
-     *
-     * ![Example](https://edejin.github.io/DGeoUtils/media/examples/findPoints.png)
-     * @param c
-     */
     findPoints(c) {
         if (this.equal(c)) {
             return Infinity;
@@ -63,12 +51,6 @@ class DCircle {
     equal({ center, r }) {
         return this.center.equal(center) && this.r === r;
     }
-    /**
-     * Transform circle to polygon
-     *
-     * ![Example](https://edejin.github.io/DGeoUtils/media/examples/findPolygonInside.png)
-     * @param [pointCount=64]
-     */
     findPolygonInside(pointCount = 64) {
         const preAngle = 2 * Math.PI / pointCount;
         const points = [];
@@ -80,18 +62,6 @@ class DCircle {
         }
         return new DPolygon_1.DPolygon([...points, points[0]]);
     }
-    /**
-     * Transform circle to polygon on sphere. It would be different for different latitude.
-     *
-     * @remarks
-     * Center should be Lng/Lat.
-     *
-     * @remarks
-     * Radius should be in meters.
-     *
-     * ![Example](https://edejin.github.io/DGeoUtils/media/examples/findPolygonInsideOnSphere.png)
-     * @param [pointCount=64]
-     */
     findPolygonInsideOnSphere(pointCount = 64) {
         (0, utils_1.checkFunction)('findPolygonInsideOnSphere')
             .checkArgument('center')

package/dist/DLine.d.ts

@@ -4,32 +4,15 @@ export declare class DLine {
     a: number;
     b: number;
     c: number;
-    p1: DPoint;
-    p2: DPoint;
-    constructor(a?: number, b?: number, c?: number, p1?: DPoint, p2?: DPoint);
+    begin: DPoint;
+    end: DPoint;
+    constructor(a: number, b: number, c: number, begin?: DPoint, end?: DPoint);
     clone(): DLine;
     findPerpendicular(p: DPoint): DLine;
     perpendicularDistance(p: DPoint): number;
-    /**
-     * Find intersection of two lines segments.
-     * For intersection of two lines use [[findPoint]]
-     * @param l
-     * @param [d=0]
-     * @param [includeOnly=false]
-     */
     intersection(l: DLine, d?: number, includeOnly?: boolean): DPoint | null;
     intersectionWithCircle(circle: DCircle): DPoint | [DPoint, DPoint] | null;
-    /**
-     * Check if point below to line segment
-     * @param p
-     * @param d
-     */
     inRange(p: DPoint, d?: number): boolean;
-    /**
-     * Check if point below to line segment, but not equal star or end point.
-     * @param p
-     * @param [d=0]
-     */
     insideRange(p: DPoint, d?: number): boolean;
     get center(): DPoint;
     get minX(): number;
@@ -38,52 +21,16 @@ export declare class DLine {
     get maxY(): number;
     toString(): string;
     getValue(): number[];
-    /**
-     * Find `x` from `y` value of point
-     * @param p
-     */
     x(p: DPoint): DPoint;
-    /**
-     * Find `y` from `x` value of point
-     * @param p
-     */
     y(p: DPoint): DPoint;
-    /**
-     * Find intersection of two lines.
-     * For intersection of two lines segments use [[intersection]]
-     * @param l
-     */
     findPoint(l: DLine): DPoint | null;
-    /**
-     * Check if line parallel to `x` or `y` axis
-     */
     get isParallel(): boolean;
     get isParallelY(): boolean;
     get isParallelX(): boolean;
-    /**
-     * Get lines segment start and end points as array
-     */
     get points(): [DPoint, DPoint];
-    /**
-     * Get line segment direction (from start point to end point)
-     */
     getFi(): number;
     toWKT(): string;
-    /**
-     * Move lines point to left or right
-     * @param p
-     * @param d
-     */
     movePoint(p: DPoint, d: number): DPoint;
-    /**
-     * Find angle between current line and line in argument
-     * @param l
-     * @param delta
-     */
-    findFi(l: DLine, delta?: number): number;
-    /**
-     * [Cross product](https://en.wikipedia.org/wiki/Cross_product)
-     * @param l
-     */
-    vectorProduct(l: DLine): DLine;
+    findFi({ a, b }: DLine, delta?: number): number;
+    vectorProduct({ a, b, c }: DLine): DLine;
 }

package/dist/DLine.js

@@ -4,48 +4,38 @@ exports.DLine = void 0;
 const DPoint_1 = require("./DPoint");
 const utils_1 = require("./utils");
 class DLine {
-    // eslint-disable-next-line no-useless-constructor
-    constructor(a = 0, b = 0, c = 0, p1 = DPoint_1.DPoint.zero(), p2 = DPoint_1.DPoint.zero()
-    // eslint-disable-next-line no-empty-function
-    ) {
+    constructor(a, b, c, begin = DPoint_1.DPoint.zero(), end = DPoint_1.DPoint.zero()) {
         this.a = a;
         this.b = b;
         this.c = c;
-        this.p1 = p1;
-        this.p2 = p2;
+        this.begin = begin;
+        this.end = end;
     }
     clone() {
-        return new DLine(this.a, this.b, this.c, this.p1.clone(), this.p2.clone());
+        return new DLine(this.a, this.b, this.c, this.begin.clone(), this.end.clone());
     }
     findPerpendicular(p) {
         (0, utils_1.checkFunction)('findPerpendicular')
-            .checkArgument('this.p1')
-            .shouldBeMeters(this.p1)
-            .checkArgument('this.p2')
-            .shouldBeMeters(this.p2)
+            .checkArgument('this.begin')
+            .shouldBeMeters(this.begin)
+            .checkArgument('this.end')
+            .shouldBeMeters(this.end)
             .checkArgument('p')
             .shouldBeMeters(p);
         return new DLine(-this.b, this.a, this.b * p.x - this.a * p.y);
     }
     perpendicularDistance(p) {
         (0, utils_1.checkFunction)('perpendicularDistance')
-            .checkArgument('this.p1')
-            .shouldBeMeters(this.p1)
-            .checkArgument('this.p2')
-            .shouldBeMeters(this.p2)
+            .checkArgument('this.begin')
+            .shouldBeMeters(this.begin)
+            .checkArgument('this.end')
+            .shouldBeMeters(this.end)
             .checkArgument('p')
             .shouldBeMeters(p);
         const perpendicularLine = this.findPerpendicular(p);
         const targetPoint = perpendicularLine.findPoint(this);
         return targetPoint.distance(p);
     }
-    /**
-     * Find intersection of two lines segments.
-     * For intersection of two lines use [[findPoint]]
-     * @param l
-     * @param [d=0]
-     * @param [includeOnly=false]
-     */
     intersection(l, d = 0, includeOnly = false) {
         const p = this.findPoint(l);
         if (p) {
@@ -61,10 +51,10 @@ class DLine {
         const per = this.findPerpendicular(center);
         const t = this.intersection(per, Infinity);
         let distance = t.distance(center);
-        if (this.p1.equal(center)) {
+        if (this.begin.equal(center)) {
             distance = 0;
         }
-        if (this.p2.equal(center)) {
+        if (this.end.equal(center)) {
             distance = 0;
         }
         if (distance < r) {
@@ -72,27 +62,25 @@ class DLine {
             if (this.isParallel) {
                 const ct = center.distance(t);
                 const move = Math.sqrt(r * r - ct * ct);
-                // Mean "|" x = const
                 if (this.isParallelY) {
-                    t.x = this.p1.x;
+                    t.x = this.begin.x;
                     const r1 = t.clone().move(0, -move);
                     const r2 = t.clone().move(0, move);
                     return [r1, r2];
                 }
-                // Mean "-" y = const
                 if (this.isParallelX) {
-                    t.y = this.p1.y;
+                    t.y = this.begin.y;
                     const r1 = t.clone().move(move, 0);
                     const r2 = t.clone().move(-move, 0);
                     return [r1, r2];
                 }
             }
-            if (this.p1.like(center)) {
-                const p = this.p1.clone();
+            if (this.begin.like(center)) {
+                const p = this.begin.clone();
                 return [this.movePoint(p, r), this.movePoint(p, -r)];
             }
-            if (this.p2.like(center)) {
-                const p = this.p2.clone();
+            if (this.end.like(center)) {
+                const p = this.end.clone();
                 return [this.movePoint(p, r), this.movePoint(p, -r)];
             }
             const s = a * a + b * b;
@@ -107,11 +95,6 @@ class DLine {
         }
         return null;
     }
-    /**
-     * Check if point below to line segment
-     * @param p
-     * @param d
-     */
     inRange(p, d = 0) {
         const { minX, minY, maxX, maxY } = this;
         const { x, y } = p;
@@ -119,22 +102,17 @@ class DLine {
         const isInY = y >= minY - d && y <= maxY + d;
         return isInX && isInY;
     }
-    /**
-     * Check if point below to line segment, but not equal star or end point.
-     * @param p
-     * @param [d=0]
-     */
     insideRange(p, d = 0) {
-        const { p1, p2 } = this;
-        return this.inRange(p, d) && !p1.like(p, 0.00001) && !p2.like(p, 0.00001);
+        const { begin, end } = this;
+        return this.inRange(p, d) && !begin.like(p, 0.00001) && !end.like(p, 0.00001);
     }
     get center() {
-        return this.p1
+        return this.begin
             .clone()
-            .setIfLessThan(this.p2)
-            .move(this.p2
+            .setIfLessThan(this.end)
+            .move(this.end
             .clone()
-            .move(this.p1
+            .move(this.begin
             .clone()
             .minus())
             .abs()
@@ -142,16 +120,16 @@ class DLine {
             .divide(2));
     }
     get minX() {
-        return Math.min(this.p1.x, this.p2.x);
+        return Math.min(this.begin.x, this.end.x);
     }
     get minY() {
-        return Math.min(this.p1.y, this.p2.y);
+        return Math.min(this.begin.y, this.end.y);
     }
     get maxX() {
-        return Math.max(this.p1.x, this.p2.x);
+        return Math.max(this.begin.x, this.end.x);
     }
     get maxY() {
-        return Math.max(this.p1.y, this.p2.y);
+        return Math.max(this.begin.y, this.end.y);
     }
     toString() {
         return `(${this.a}, ${this.b}, ${this.c})`;
@@ -159,10 +137,6 @@ class DLine {
     getValue() {
         return [this.a, this.b, this.c];
     }
-    /**
-     * Find `x` from `y` value of point
-     * @param p
-     */
     x(p) {
         if (this.isParallelY) {
             return new DPoint_1.DPoint(-this.c / this.a, p.y);
@@ -172,10 +146,6 @@ class DLine {
         }
         return new DPoint_1.DPoint(-this.b / this.a * p.y - this.c / this.a, p.y);
     }
-    /**
-     * Find `y` from `x` value of point
-     * @param p
-     */
     y(p) {
         if (this.isParallelY) {
             return new DPoint_1.DPoint(-this.c / this.a, p.y);
@@ -185,11 +155,6 @@ class DLine {
         }
         return new DPoint_1.DPoint(p.x, -this.a / this.b * p.x - this.c / this.b);
     }
-    /**
-     * Find intersection of two lines.
-     * For intersection of two lines segments use [[intersection]]
-     * @param l
-     */
     findPoint(l) {
         if (this.isParallelY && l.isParallelY) {
             return null;
@@ -225,9 +190,6 @@ class DLine {
         }
         return res;
     }
-    /**
-     * Check if line parallel to `x` or `y` axis
-     */
     get isParallel() {
         return this.isParallelX || this.isParallelY;
     }
@@ -237,61 +199,29 @@ class DLine {
     get isParallelX() {
         return Math.abs(this.a) < 0.001;
     }
-    /**
-     * Get lines segment start and end points as array
-     */
     get points() {
-        return [this.p1, this.p2];
+        return [this.begin, this.end];
     }
-    /**
-     * Get line segment direction (from start point to end point)
-     */
     getFi() {
         (0, utils_1.checkFunction)('getFi')
-            .checkArgument('this.p1')
-            .shouldBeMeters(this.p1)
-            .checkArgument('this.p2')
-            .shouldBeMeters(this.p2);
-        const l = new DLine(0, 1, 0);
-        const result = this.findFi(l);
-        if (this.p1.x === this.p2.x) {
-            if (this.p1.y === this.p2.y) {
-                return 0;
-            }
-            else if (this.p1.y < this.p2.y) {
-                return Math.PI + Math.PI / 2;
-            }
-            return Math.PI / 2;
-        }
-        else if (this.p1.x < this.p2.x) {
-            if (this.p1.y === this.p2.y) {
-                return 0;
-            }
-            else if (this.p1.y < this.p2.y) {
-                return Math.PI - result + Math.PI;
-            }
-            return result;
-        }
-        if (this.p1.y === this.p2.y) {
-            return Math.PI;
-        }
-        else if (this.p1.y < this.p2.y) {
-            return Math.PI - result + Math.PI;
+            .checkArgument('this.begin')
+            .shouldBeMeters(this.begin)
+            .checkArgument('this.end')
+            .shouldBeMeters(this.end);
+        const { x, y } = this.end.clone().move(this.begin.clone().minus());
+        let v = Math.atan2(y, x) - Math.PI;
+        if (v > 0) {
+            v = Math.PI - v;
         }
-        return result;
+        return (Math.PI - v) % (Math.PI * 2);
     }
     toWKT() {
-        const { p1: { x: x1, y: y1 }, p2: { x: x2, y: y2 } } = this;
+        const { begin: { x: x1, y: y1 }, end: { x: x2, y: y2 } } = this;
         return `LINESTRING (${x1} ${y1}, ${x2} ${y2})`;
     }
-    /**
-     * Move lines point to left or right
-     * @param p
-     * @param d
-     */
     movePoint(p, d) {
         const fi = this.findFi(new DLine(1, 0, 0));
-        const td = this.p1.distance(this.p2) / 2;
+        const td = this.begin.distance(this.end) / 2;
         const dcosT = td * Math.cos(fi);
         const dsinT = td * Math.sin(fi);
         const p1T = new DPoint_1.DPoint(p.x - dsinT, p.y - dcosT);
@@ -305,13 +235,9 @@ class DLine {
         }
         return p3;
     }
-    /**
-     * Find angle between current line and line in argument
-     * @param l
-     * @param delta
-     */
-    findFi(l, delta = 1.0001) {
-        let val = (this.a * l.a + this.b * l.b) / (Math.sqrt(this.a * this.a + this.b * this.b) * Math.sqrt(l.a * l.a + l.b * l.b));
+    findFi({ a, b }, delta = 1.0001) {
+        const { a: q, b: w } = this;
+        let val = (q * a + w * b) / (Math.sqrt(q * q + w * w) * Math.sqrt(a * a + b * b));
         if (val > 1 && val < delta) {
             val = 1;
         }
@@ -320,15 +246,9 @@ class DLine {
         }
         return Math.acos(val);
     }
-    /**
-     * [Cross product](https://en.wikipedia.org/wiki/Cross_product)
-     * @param l
-     */
-    vectorProduct(l) {
-        const i = this.b * l.c - this.c * l.b;
-        const j = this.c * l.a - this.a * l.c;
-        const k = this.a * l.b - this.b * l.a;
-        return new DLine(i, j, k);
+    vectorProduct({ a, b, c }) {
+        const { a: q, b: w, c: e } = this;
+        return new DLine(w * c - e * b, e * a - q * c, q * b - w * a);
     }
 }
 exports.DLine = DLine;