oikan 0.0.2.4__tar.gz → 0.0.2.5__tar.gz
This diff represents the content of publicly available package versions that have been released to one of the supported registries. The information contained in this diff is provided for informational purposes only and reflects changes between package versions as they appear in their respective public registries.
- {oikan-0.0.2.4 → oikan-0.0.2.5}/PKG-INFO +12 -31
- {oikan-0.0.2.4 → oikan-0.0.2.5}/README.md +11 -30
- {oikan-0.0.2.4 → oikan-0.0.2.5}/oikan/model.py +29 -8
- {oikan-0.0.2.4 → oikan-0.0.2.5}/oikan/utils.py +21 -9
- {oikan-0.0.2.4 → oikan-0.0.2.5}/oikan.egg-info/PKG-INFO +12 -31
- {oikan-0.0.2.4 → oikan-0.0.2.5}/oikan.egg-info/SOURCES.txt +0 -1
- {oikan-0.0.2.4 → oikan-0.0.2.5}/pyproject.toml +1 -1
- oikan-0.0.2.4/oikan/symbolic.py +0 -28
- {oikan-0.0.2.4 → oikan-0.0.2.5}/LICENSE +0 -0
- {oikan-0.0.2.4 → oikan-0.0.2.5}/oikan/__init__.py +0 -0
- {oikan-0.0.2.4 → oikan-0.0.2.5}/oikan/exceptions.py +0 -0
- {oikan-0.0.2.4 → oikan-0.0.2.5}/oikan.egg-info/dependency_links.txt +0 -0
- {oikan-0.0.2.4 → oikan-0.0.2.5}/oikan.egg-info/requires.txt +0 -0
- {oikan-0.0.2.4 → oikan-0.0.2.5}/oikan.egg-info/top_level.txt +0 -0
- {oikan-0.0.2.4 → oikan-0.0.2.5}/setup.cfg +0 -0
- {oikan-0.0.2.4 → oikan-0.0.2.5}/setup.py +0 -0
|
@@ -1,6 +1,6 @@
|
|
|
1
1
|
Metadata-Version: 2.4
|
|
2
2
|
Name: oikan
|
|
3
|
-
Version: 0.0.2.
|
|
3
|
+
Version: 0.0.2.5
|
|
4
4
|
Summary: OIKAN: Optimized Interpretable Kolmogorov-Arnold Networks
|
|
5
5
|
Author: Arman Zhalgasbayev
|
|
6
6
|
License: MIT
|
|
@@ -66,6 +66,17 @@ OIKAN implements the Kolmogorov-Arnold Representation Theorem through a novel ne
|
|
|
66
66
|
return combine_weighted_outputs(edge_outputs, self.weights)
|
|
67
67
|
```
|
|
68
68
|
|
|
69
|
+
3. **Basis functions**
|
|
70
|
+
```python
|
|
71
|
+
# Edge activation contains interpretable basis functions
|
|
72
|
+
ADVANCED_LIB = {
|
|
73
|
+
'x': (lambda x: x), # Linear
|
|
74
|
+
'x^2': (lambda x: x**2), # Quadratic
|
|
75
|
+
'sin(x)': np.sin, # Periodic
|
|
76
|
+
'tanh(x)': np.tanh # Bounded
|
|
77
|
+
}
|
|
78
|
+
```
|
|
79
|
+
|
|
69
80
|
## Quick Start
|
|
70
81
|
|
|
71
82
|
### Installation
|
|
@@ -126,36 +137,6 @@ model.save_symbolic_formula("classification_formula.txt")
|
|
|
126
137
|
|
|
127
138
|
*Example of the saved symbolic formula instructions: [outputs/classification_symbolic_formula.txt](outputs/classification_symbolic_formula.txt)*
|
|
128
139
|
|
|
129
|
-
|
|
130
|
-
### Key Design Principles
|
|
131
|
-
|
|
132
|
-
1. **Interpretability by Design**
|
|
133
|
-
```python
|
|
134
|
-
# Edge activation contains interpretable basis functions
|
|
135
|
-
ADVANCED_LIB = {
|
|
136
|
-
'x': (lambda x: x), # Linear
|
|
137
|
-
'x^2': (lambda x: x**2), # Quadratic
|
|
138
|
-
'sin(x)': np.sin, # Periodic
|
|
139
|
-
'tanh(x)': np.tanh # Bounded
|
|
140
|
-
}
|
|
141
|
-
```
|
|
142
|
-
|
|
143
|
-
2. **Automatic Simplification**
|
|
144
|
-
```python
|
|
145
|
-
def simplify_formula(terms, threshold=1e-4):
|
|
146
|
-
return [term for term in terms if abs(term.coefficient) > threshold]
|
|
147
|
-
```
|
|
148
|
-
|
|
149
|
-
3. **Research-Oriented Architecture**
|
|
150
|
-
```python
|
|
151
|
-
class SymbolicEdge:
|
|
152
|
-
def forward(self, x):
|
|
153
|
-
return sum(w * f(x) for w, f in zip(self.weights, self.basis_functions))
|
|
154
|
-
|
|
155
|
-
def get_formula(self):
|
|
156
|
-
return format_symbolic_terms(self.weights, self.basis_functions)
|
|
157
|
-
```
|
|
158
|
-
|
|
159
140
|
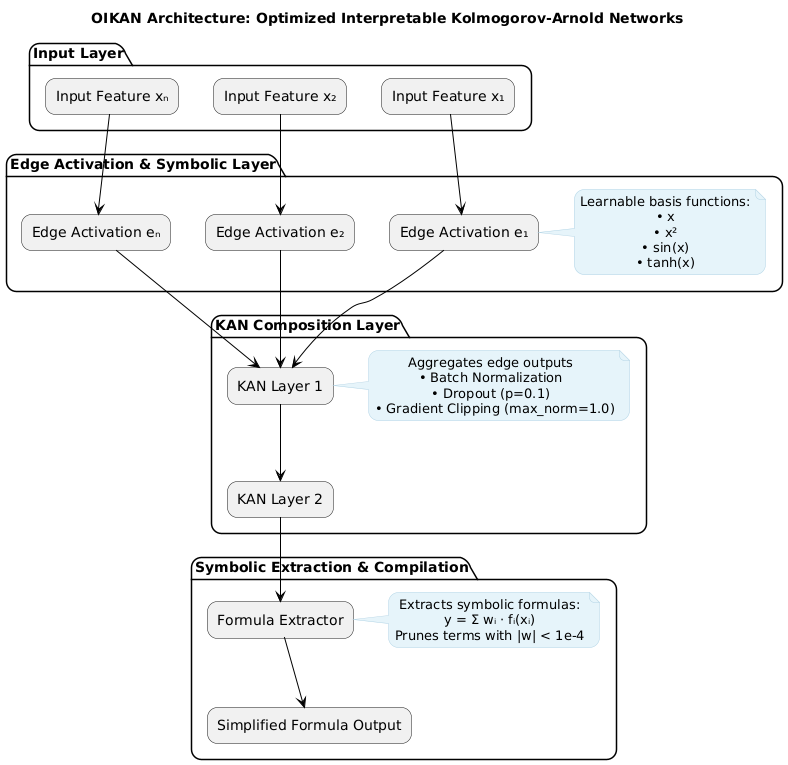
### Architecture Diagram
|
|
160
141
|
|
|
161
142
|
|
|
@@ -49,6 +49,17 @@ OIKAN implements the Kolmogorov-Arnold Representation Theorem through a novel ne
|
|
|
49
49
|
return combine_weighted_outputs(edge_outputs, self.weights)
|
|
50
50
|
```
|
|
51
51
|
|
|
52
|
+
3. **Basis functions**
|
|
53
|
+
```python
|
|
54
|
+
# Edge activation contains interpretable basis functions
|
|
55
|
+
ADVANCED_LIB = {
|
|
56
|
+
'x': (lambda x: x), # Linear
|
|
57
|
+
'x^2': (lambda x: x**2), # Quadratic
|
|
58
|
+
'sin(x)': np.sin, # Periodic
|
|
59
|
+
'tanh(x)': np.tanh # Bounded
|
|
60
|
+
}
|
|
61
|
+
```
|
|
62
|
+
|
|
52
63
|
## Quick Start
|
|
53
64
|
|
|
54
65
|
### Installation
|
|
@@ -109,36 +120,6 @@ model.save_symbolic_formula("classification_formula.txt")
|
|
|
109
120
|
|
|
110
121
|
*Example of the saved symbolic formula instructions: [outputs/classification_symbolic_formula.txt](outputs/classification_symbolic_formula.txt)*
|
|
111
122
|
|
|
112
|
-
|
|
113
|
-
### Key Design Principles
|
|
114
|
-
|
|
115
|
-
1. **Interpretability by Design**
|
|
116
|
-
```python
|
|
117
|
-
# Edge activation contains interpretable basis functions
|
|
118
|
-
ADVANCED_LIB = {
|
|
119
|
-
'x': (lambda x: x), # Linear
|
|
120
|
-
'x^2': (lambda x: x**2), # Quadratic
|
|
121
|
-
'sin(x)': np.sin, # Periodic
|
|
122
|
-
'tanh(x)': np.tanh # Bounded
|
|
123
|
-
}
|
|
124
|
-
```
|
|
125
|
-
|
|
126
|
-
2. **Automatic Simplification**
|
|
127
|
-
```python
|
|
128
|
-
def simplify_formula(terms, threshold=1e-4):
|
|
129
|
-
return [term for term in terms if abs(term.coefficient) > threshold]
|
|
130
|
-
```
|
|
131
|
-
|
|
132
|
-
3. **Research-Oriented Architecture**
|
|
133
|
-
```python
|
|
134
|
-
class SymbolicEdge:
|
|
135
|
-
def forward(self, x):
|
|
136
|
-
return sum(w * f(x) for w, f in zip(self.weights, self.basis_functions))
|
|
137
|
-
|
|
138
|
-
def get_formula(self):
|
|
139
|
-
return format_symbolic_terms(self.weights, self.basis_functions)
|
|
140
|
-
```
|
|
141
|
-
|
|
142
123
|
### Architecture Diagram
|
|
143
124
|
|
|
144
125
|

|
|
@@ -196,30 +196,51 @@ class BaseOIKAN(BaseEstimator):
|
|
|
196
196
|
def _eval_formula(self, formula, x):
|
|
197
197
|
"""Helper to evaluate a symbolic formula for an input vector x using ADVANCED_LIB basis functions."""
|
|
198
198
|
import re
|
|
199
|
-
|
|
199
|
+
from .utils import ensure_tensor
|
|
200
|
+
|
|
201
|
+
if isinstance(x, (list, tuple)):
|
|
202
|
+
x = np.array(x)
|
|
203
|
+
|
|
204
|
+
total = torch.zeros_like(ensure_tensor(x))
|
|
200
205
|
pattern = re.compile(r"(-?\d+\.\d+)\*?([\w\(\)\^]+)")
|
|
201
206
|
matches = pattern.findall(formula)
|
|
207
|
+
|
|
202
208
|
for coef_str, func_name in matches:
|
|
203
209
|
try:
|
|
204
210
|
coef = float(coef_str)
|
|
205
211
|
for key, (notation, func) in ADVANCED_LIB.items():
|
|
206
212
|
if notation.strip() == func_name.strip():
|
|
207
|
-
|
|
213
|
+
result = func(x)
|
|
214
|
+
if isinstance(result, torch.Tensor):
|
|
215
|
+
total += coef * result
|
|
216
|
+
else:
|
|
217
|
+
total += coef * ensure_tensor(result)
|
|
208
218
|
break
|
|
209
|
-
except Exception:
|
|
219
|
+
except Exception as e:
|
|
220
|
+
print(f"Warning: Error evaluating term {coef_str}*{func_name}: {str(e)}")
|
|
210
221
|
continue
|
|
211
|
-
|
|
222
|
+
|
|
223
|
+
return total.cpu().numpy() if isinstance(total, torch.Tensor) else total
|
|
212
224
|
|
|
213
225
|
def symbolic_predict(self, X):
|
|
214
226
|
"""Predict using only the extracted symbolic formula (regressor)."""
|
|
215
227
|
if not self._is_fitted:
|
|
216
228
|
raise NotFittedError("Model must be fitted before prediction")
|
|
229
|
+
|
|
217
230
|
X = np.array(X) if not isinstance(X, np.ndarray) else X
|
|
218
|
-
formulas = self.get_symbolic_formula()
|
|
231
|
+
formulas = self.get_symbolic_formula()
|
|
219
232
|
predictions = np.zeros((X.shape[0], 1))
|
|
220
|
-
|
|
221
|
-
|
|
222
|
-
|
|
233
|
+
|
|
234
|
+
try:
|
|
235
|
+
for i, formula in enumerate(formulas):
|
|
236
|
+
x = X[:, i]
|
|
237
|
+
pred = self._eval_formula(formula, x)
|
|
238
|
+
if isinstance(pred, torch.Tensor):
|
|
239
|
+
pred = pred.cpu().numpy()
|
|
240
|
+
predictions[:, 0] += pred
|
|
241
|
+
except Exception as e:
|
|
242
|
+
raise RuntimeError(f"Error in symbolic prediction: {str(e)}")
|
|
243
|
+
|
|
223
244
|
return predictions
|
|
224
245
|
|
|
225
246
|
def compile_symbolic_formula(self, filename="output/final_symbolic_formula.txt"):
|
|
@@ -3,35 +3,47 @@ import torch
|
|
|
3
3
|
import torch.nn as nn
|
|
4
4
|
import numpy as np
|
|
5
5
|
|
|
6
|
+
def ensure_tensor(x):
|
|
7
|
+
"""Helper function to ensure input is a PyTorch tensor."""
|
|
8
|
+
if isinstance(x, np.ndarray):
|
|
9
|
+
return torch.from_numpy(x).float()
|
|
10
|
+
elif isinstance(x, (int, float)):
|
|
11
|
+
return torch.tensor([x], dtype=torch.float32)
|
|
12
|
+
elif isinstance(x, torch.Tensor):
|
|
13
|
+
return x.float()
|
|
14
|
+
else:
|
|
15
|
+
raise ValueError(f"Unsupported input type: {type(x)}")
|
|
16
|
+
|
|
17
|
+
# Updated to handle numpy arrays and scalars
|
|
6
18
|
ADVANCED_LIB = {
|
|
7
|
-
'x':
|
|
8
|
-
'x^2':
|
|
9
|
-
'sin':
|
|
10
|
-
'tanh': ('tanh(x)', lambda x:
|
|
19
|
+
'x': ('x', lambda x: ensure_tensor(x)),
|
|
20
|
+
'x^2': ('x^2', lambda x: torch.pow(ensure_tensor(x), 2)),
|
|
21
|
+
'sin': ('sin(x)', lambda x: torch.sin(ensure_tensor(x))),
|
|
22
|
+
'tanh': ('tanh(x)', lambda x: torch.tanh(ensure_tensor(x)))
|
|
11
23
|
}
|
|
12
24
|
|
|
13
25
|
class EdgeActivation(nn.Module):
|
|
14
|
-
"""Learnable edge-based activation function."""
|
|
26
|
+
"""Learnable edge-based activation function with improved gradient flow."""
|
|
15
27
|
def __init__(self):
|
|
16
28
|
super().__init__()
|
|
17
29
|
self.weights = nn.Parameter(torch.randn(len(ADVANCED_LIB)))
|
|
18
30
|
self.bias = nn.Parameter(torch.zeros(1))
|
|
19
31
|
|
|
20
32
|
def forward(self, x):
|
|
33
|
+
x_tensor = ensure_tensor(x)
|
|
21
34
|
features = []
|
|
22
35
|
for _, func in ADVANCED_LIB.values():
|
|
23
|
-
feat =
|
|
24
|
-
dtype=torch.float32).to(x.device)
|
|
36
|
+
feat = func(x_tensor)
|
|
25
37
|
features.append(feat)
|
|
26
38
|
features = torch.stack(features, dim=-1)
|
|
27
39
|
return torch.matmul(features, self.weights.unsqueeze(0).T) + self.bias
|
|
28
40
|
|
|
29
41
|
def get_symbolic_repr(self, threshold=1e-4):
|
|
30
42
|
"""Get symbolic representation of the activation function."""
|
|
43
|
+
weights_np = self.weights.detach().cpu().numpy()
|
|
31
44
|
significant_terms = []
|
|
32
45
|
|
|
33
|
-
for (notation, _), weight in zip(ADVANCED_LIB.values(),
|
|
34
|
-
self.weights.detach().cpu().numpy()):
|
|
46
|
+
for (notation, _), weight in zip(ADVANCED_LIB.values(), weights_np):
|
|
35
47
|
if abs(weight) > threshold:
|
|
36
48
|
significant_terms.append(f"{weight:.4f}*{notation}")
|
|
37
49
|
|
|
@@ -1,6 +1,6 @@
|
|
|
1
1
|
Metadata-Version: 2.4
|
|
2
2
|
Name: oikan
|
|
3
|
-
Version: 0.0.2.
|
|
3
|
+
Version: 0.0.2.5
|
|
4
4
|
Summary: OIKAN: Optimized Interpretable Kolmogorov-Arnold Networks
|
|
5
5
|
Author: Arman Zhalgasbayev
|
|
6
6
|
License: MIT
|
|
@@ -66,6 +66,17 @@ OIKAN implements the Kolmogorov-Arnold Representation Theorem through a novel ne
|
|
|
66
66
|
return combine_weighted_outputs(edge_outputs, self.weights)
|
|
67
67
|
```
|
|
68
68
|
|
|
69
|
+
3. **Basis functions**
|
|
70
|
+
```python
|
|
71
|
+
# Edge activation contains interpretable basis functions
|
|
72
|
+
ADVANCED_LIB = {
|
|
73
|
+
'x': (lambda x: x), # Linear
|
|
74
|
+
'x^2': (lambda x: x**2), # Quadratic
|
|
75
|
+
'sin(x)': np.sin, # Periodic
|
|
76
|
+
'tanh(x)': np.tanh # Bounded
|
|
77
|
+
}
|
|
78
|
+
```
|
|
79
|
+
|
|
69
80
|
## Quick Start
|
|
70
81
|
|
|
71
82
|
### Installation
|
|
@@ -126,36 +137,6 @@ model.save_symbolic_formula("classification_formula.txt")
|
|
|
126
137
|
|
|
127
138
|
*Example of the saved symbolic formula instructions: [outputs/classification_symbolic_formula.txt](outputs/classification_symbolic_formula.txt)*
|
|
128
139
|
|
|
129
|
-
|
|
130
|
-
### Key Design Principles
|
|
131
|
-
|
|
132
|
-
1. **Interpretability by Design**
|
|
133
|
-
```python
|
|
134
|
-
# Edge activation contains interpretable basis functions
|
|
135
|
-
ADVANCED_LIB = {
|
|
136
|
-
'x': (lambda x: x), # Linear
|
|
137
|
-
'x^2': (lambda x: x**2), # Quadratic
|
|
138
|
-
'sin(x)': np.sin, # Periodic
|
|
139
|
-
'tanh(x)': np.tanh # Bounded
|
|
140
|
-
}
|
|
141
|
-
```
|
|
142
|
-
|
|
143
|
-
2. **Automatic Simplification**
|
|
144
|
-
```python
|
|
145
|
-
def simplify_formula(terms, threshold=1e-4):
|
|
146
|
-
return [term for term in terms if abs(term.coefficient) > threshold]
|
|
147
|
-
```
|
|
148
|
-
|
|
149
|
-
3. **Research-Oriented Architecture**
|
|
150
|
-
```python
|
|
151
|
-
class SymbolicEdge:
|
|
152
|
-
def forward(self, x):
|
|
153
|
-
return sum(w * f(x) for w, f in zip(self.weights, self.basis_functions))
|
|
154
|
-
|
|
155
|
-
def get_formula(self):
|
|
156
|
-
return format_symbolic_terms(self.weights, self.basis_functions)
|
|
157
|
-
```
|
|
158
|
-
|
|
159
140
|
### Architecture Diagram
|
|
160
141
|
|
|
161
142
|

|
oikan-0.0.2.4/oikan/symbolic.py
DELETED
|
@@ -1,28 +0,0 @@
|
|
|
1
|
-
from .utils import ADVANCED_LIB
|
|
2
|
-
|
|
3
|
-
def symbolic_edge_repr(weights, bias=None, threshold=1e-4):
|
|
4
|
-
"""
|
|
5
|
-
Given a list of weights (floats) and an optional bias,
|
|
6
|
-
returns a list of structured terms (coefficient, basis function string).
|
|
7
|
-
"""
|
|
8
|
-
terms = []
|
|
9
|
-
# weights should be in the same order as ADVANCED_LIB.items()
|
|
10
|
-
for (_, (notation, _)), w in zip(ADVANCED_LIB.items(), weights):
|
|
11
|
-
if abs(w) > threshold:
|
|
12
|
-
terms.append((w, notation))
|
|
13
|
-
if bias is not None and abs(bias) > threshold:
|
|
14
|
-
# use "1" to represent the constant term
|
|
15
|
-
terms.append((bias, "1"))
|
|
16
|
-
return terms
|
|
17
|
-
|
|
18
|
-
def format_symbolic_terms(terms):
|
|
19
|
-
"""
|
|
20
|
-
Formats a list of structured symbolic terms (coef, basis) to a string.
|
|
21
|
-
"""
|
|
22
|
-
formatted_terms = []
|
|
23
|
-
for coef, basis in terms:
|
|
24
|
-
if basis == "1":
|
|
25
|
-
formatted_terms.append(f"{coef:.4f}")
|
|
26
|
-
else:
|
|
27
|
-
formatted_terms.append(f"{coef:.4f}*{basis}")
|
|
28
|
-
return " + ".join(formatted_terms) if formatted_terms else "0"
|
|
File without changes
|
|
File without changes
|
|
File without changes
|
|
File without changes
|
|
File without changes
|
|
File without changes
|
|
File without changes
|
|
File without changes
|