cdc-cluster 0.1.1__tar.gz → 0.2.1__tar.gz
This diff represents the content of publicly available package versions that have been released to one of the supported registries. The information contained in this diff is provided for informational purposes only and reflects changes between package versions as they appear in their respective public registries.
- cdc_cluster-0.2.1/LICENSE +21 -0
- {cdc_cluster-0.1.1 → cdc_cluster-0.2.1}/PKG-INFO +39 -60
- cdc_cluster-0.2.1/README.md +74 -0
- cdc_cluster-0.2.1/cdc_cluster/__init__.py +3 -0
- cdc_cluster-0.2.1/cdc_cluster/_cdc.py +262 -0
- {cdc_cluster-0.1.1 → cdc_cluster-0.2.1}/cdc_cluster.egg-info/PKG-INFO +39 -60
- {cdc_cluster-0.1.1 → cdc_cluster-0.2.1}/cdc_cluster.egg-info/SOURCES.txt +4 -2
- cdc_cluster-0.2.1/cdc_cluster.egg-info/top_level.txt +1 -0
- {cdc_cluster-0.1.1 → cdc_cluster-0.2.1}/pyproject.toml +11 -3
- cdc_cluster-0.2.1/tests/test_cdc.py +50 -0
- cdc_cluster-0.1.1/README.md +0 -96
- cdc_cluster-0.1.1/cdc/__init__.py +0 -193
- cdc_cluster-0.1.1/cdc_cluster.egg-info/top_level.txt +0 -1
- cdc_cluster-0.1.1/test/test1.py +0 -6
- {cdc_cluster-0.1.1 → cdc_cluster-0.2.1}/cdc_cluster.egg-info/dependency_links.txt +0 -0
- {cdc_cluster-0.1.1 → cdc_cluster-0.2.1}/cdc_cluster.egg-info/requires.txt +0 -0
- {cdc_cluster-0.1.1 → cdc_cluster-0.2.1}/setup.cfg +0 -0
|
@@ -0,0 +1,21 @@
|
|
|
1
|
+
MIT License
|
|
2
|
+
|
|
3
|
+
Copyright (c) 2024 ZPGuiGroupWhu
|
|
4
|
+
|
|
5
|
+
Permission is hereby granted, free of charge, to any person obtaining a copy
|
|
6
|
+
of this software and associated documentation files (the "Software"), to deal
|
|
7
|
+
in the Software without restriction, including without limitation the rights
|
|
8
|
+
to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
|
|
9
|
+
copies of the Software, and to permit persons to whom the Software is
|
|
10
|
+
furnished to do so, subject to the following conditions:
|
|
11
|
+
|
|
12
|
+
The above copyright notice and this permission notice shall be included in all
|
|
13
|
+
copies or substantial portions of the Software.
|
|
14
|
+
|
|
15
|
+
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
|
|
16
|
+
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
|
|
17
|
+
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
|
|
18
|
+
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
|
|
19
|
+
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
|
|
20
|
+
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
|
|
21
|
+
SOFTWARE.
|
|
@@ -1,6 +1,6 @@
|
|
|
1
1
|
Metadata-Version: 2.1
|
|
2
2
|
Name: cdc-cluster
|
|
3
|
-
Version: 0.
|
|
3
|
+
Version: 0.2.1
|
|
4
4
|
Summary: A novel Clustering algorithm by measuring Direction Centrality (CDC) locally. It adopts a density-independent metric based on the distribution of K-nearest neighbors (KNNs) to distinguish between internal and boundary points. The boundary points generate enclosed cages to bind the connections of internal points.
|
|
5
5
|
Author-email: pdh <pengdh@whu.edu.cn>
|
|
6
6
|
Project-URL: Homepage, https://github.com/ZPGuiGroupWhu/CDC-pkg
|
|
@@ -20,6 +20,7 @@ Classifier: Programming Language :: Python :: 3.11
|
|
|
20
20
|
Classifier: Programming Language :: Python :: 3.12
|
|
21
21
|
Requires-Python: >=3.8
|
|
22
22
|
Description-Content-Type: text/markdown
|
|
23
|
+
License-File: LICENSE
|
|
23
24
|
Requires-Dist: scikit-learn>=1.3.2
|
|
24
25
|
|
|
25
26
|
# Clustering by measuring local direction centrality for data with heterogeneous density and weak connectivity (CDC)
|
|
@@ -46,71 +47,49 @@ cd CDC-pkg
|
|
|
46
47
|
pip install -e .
|
|
47
48
|
```
|
|
48
49
|
|
|
49
|
-
#
|
|
50
|
-
The CDC algorithm
|
|
50
|
+
# Usage
|
|
51
|
+
The CDC algorithm is refactored to be a scikit-learn compatible estimator. It provides both a class-based interface `CDC` and a function-based interface `cdc_cluster`.
|
|
51
52
|
|
|
52
|
-
|
|
53
|
+
### Class-based Usage
|
|
53
54
|
```python
|
|
54
|
-
|
|
55
|
-
"""Clustering by measuring local Direction Centrality (CDC) algorithm.
|
|
56
|
-
|
|
57
|
-
This function implements the CDC clustering algorithm, which is a connectivity-based
|
|
58
|
-
clustering method that identifies boundary points using a directional centrality
|
|
59
|
-
metric (DCM) and connects internal points to generate cluster labels. DCM is defined
|
|
60
|
-
as angle variance in 2D space and simplex volume variance in higher dimensions.
|
|
61
|
-
|
|
62
|
-
The algorithm works in several steps:
|
|
63
|
-
1. For each point, find k-nearest neighbors
|
|
64
|
-
2. For each point, calculate its DCM
|
|
65
|
-
3. Identify boundary and internal points based on the DCM threshold
|
|
66
|
-
4. Calculate reachable distances of the internal points
|
|
67
|
-
5. Form clusters by connecting nearby internal points
|
|
68
|
-
6. Assign boundary points to nearest clusters
|
|
69
|
-
|
|
70
|
-
Args:
|
|
71
|
-
X (np.ndarray): Input data matrix of shape (n_samples, n_features).
|
|
72
|
-
Each row represents a data point and each column represents a feature.
|
|
73
|
-
k_num (int): Number of nearest neighbors to consider. Must be greater than 0.
|
|
74
|
-
This parameter controls the local neighborhood size.
|
|
75
|
-
ratio (float): Ratio for determining the DCM threshold. Must be between 0 and 1.
|
|
76
|
-
Lower values result in fewer internal points and more boundary points.
|
|
77
|
-
|
|
78
|
-
Returns:
|
|
79
|
-
np.ndarray: Cluster labels for each data point. Shape (n_samples,).
|
|
80
|
-
Labels are integers starting from 1, where points with the same label
|
|
81
|
-
belong to the same cluster.
|
|
82
|
-
|
|
83
|
-
Raises:
|
|
84
|
-
AssertionError: If k_num <= 0 or ratio is not in (0, 1).
|
|
85
|
-
ValueError: If X is not a 2D array or has insufficient data points.
|
|
86
|
-
|
|
87
|
-
Note:
|
|
88
|
-
- For 2D data, the algorithm uses angle variance between k-nearest neighbors
|
|
89
|
-
- For higher dimensional data, it uses convex hull simplex volume variance
|
|
90
|
-
- The algorithm automatically handles edge cases and numerical instabilities
|
|
91
|
-
"""
|
|
92
|
-
```
|
|
93
|
-
After installing the CDC library, you can use this function as follows:
|
|
94
|
-
```python
|
|
95
|
-
from cdc import cdc_cluster
|
|
55
|
+
from cdc_cluster import CDC
|
|
96
56
|
import numpy as np
|
|
97
|
-
import pandas as pd
|
|
98
57
|
import matplotlib.pyplot as plt
|
|
99
|
-
import
|
|
100
|
-
|
|
101
|
-
|
|
102
|
-
X =
|
|
103
|
-
|
|
104
|
-
|
|
105
|
-
|
|
106
|
-
|
|
107
|
-
|
|
108
|
-
|
|
109
|
-
|
|
110
|
-
|
|
111
|
-
|
|
58
|
+
from sklearn.datasets import make_moons
|
|
59
|
+
|
|
60
|
+
# Generate sample data
|
|
61
|
+
X, _ = make_moons(n_samples=200, noise=0.05, random_state=42)
|
|
62
|
+
|
|
63
|
+
# Initialize and fit CDC
|
|
64
|
+
# n_neighbors: Number of nearest neighbors to consider (k_num)
|
|
65
|
+
# ratio: Ratio for determining the DCM threshold
|
|
66
|
+
cdc = CDC(n_neighbors=20, ratio=0.9)
|
|
67
|
+
cdc.fit(X)
|
|
68
|
+
|
|
69
|
+
# Get cluster labels
|
|
70
|
+
# Labels start from 0. Noisy samples are labeled as -1.
|
|
71
|
+
labels = cdc.labels_
|
|
72
|
+
|
|
73
|
+
# Plot result
|
|
74
|
+
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')
|
|
75
|
+
plt.title("CDC Clustering Result")
|
|
112
76
|
plt.show()
|
|
113
77
|
```
|
|
78
|
+
|
|
79
|
+
### Function-based Usage
|
|
80
|
+
```python
|
|
81
|
+
from cdc_cluster import cdc_cluster
|
|
82
|
+
from sklearn.datasets import make_blobs
|
|
83
|
+
|
|
84
|
+
X, _ = make_blobs(n_samples=200, centers=3, random_state=42)
|
|
85
|
+
|
|
86
|
+
# Compute clustering directly
|
|
87
|
+
# Returns an array of cluster labels
|
|
88
|
+
labels = cdc_cluster(X, n_neighbors=20, ratio=0.9)
|
|
89
|
+
|
|
90
|
+
print(f"Number of clusters: {len(set(labels)) - (1 if -1 in labels else 0)}")
|
|
91
|
+
```
|
|
92
|
+
|
|
114
93
|
# Citation Request:
|
|
115
94
|
Peng, D., Gui, Z.*, Wang, D. et al. Clustering by measuring local direction centrality for data with heterogeneous density and weak connectivity. Nat. Commun. 13, 5455 (2022).
|
|
116
95
|
https://www.nature.com/articles/s41467-022-33136-9
|
|
@@ -0,0 +1,74 @@
|
|
|
1
|
+
# Clustering by measuring local direction centrality for data with heterogeneous density and weak connectivity (CDC)
|
|
2
|
+
|
|
3
|
+
|
|
4
|
+
We propose a novel Clustering algorithm by measuring Direction Centrality (CDC) locally. It adopts a density-independent metric based on the distribution of K-nearest neighbors (KNNs) to distinguish between internal and boundary points. The boundary points generate enclosed cages to bind the connections of internal points, thereby preventing cross-cluster connections and separating weakly-connected clusters. We present an interactive ***Demo*** and a brief introduction to the algorithm at ***https://zpguigroupwhu.github.io/CDC-Introduction-Website/***, and develop a CDC toolkit at ***https://github.com/ZPGuiGroupWhu/ClusteringDirectionCentrality*** This paper has been published in ***Nature Communications***, and more details can be seen https://www.nature.com/articles/s41467-022-33136-9.
|
|
5
|
+
|
|
6
|
+
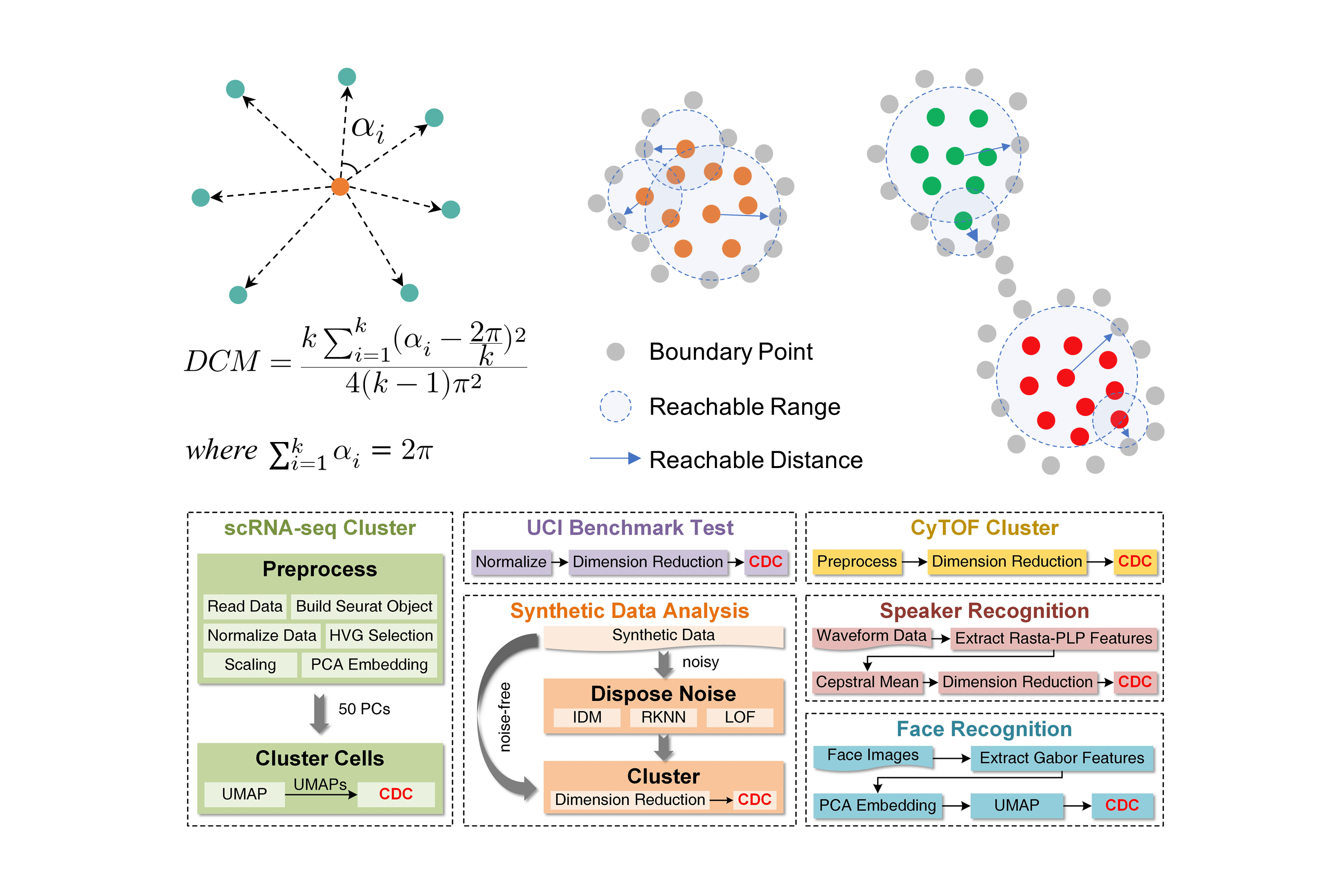
|
|
7
|
+
|
|
8
|
+
# Installation
|
|
9
|
+
Supported `python` versions are `3.8` and above.
|
|
10
|
+
|
|
11
|
+
This project has been uploaded to [PyPI](https://pypi.org/project/cdc-cluster/), supporting direct download and installation from pypi
|
|
12
|
+
|
|
13
|
+
```
|
|
14
|
+
pip install cdc-cluster
|
|
15
|
+
```
|
|
16
|
+
|
|
17
|
+
## Manual Installation
|
|
18
|
+
|
|
19
|
+
```
|
|
20
|
+
git clone https://github.com/ZPGuiGroupWhu/CDC-pkg.git
|
|
21
|
+
cd CDC-pkg
|
|
22
|
+
pip install -e .
|
|
23
|
+
```
|
|
24
|
+
|
|
25
|
+
# Usage
|
|
26
|
+
The CDC algorithm is refactored to be a scikit-learn compatible estimator. It provides both a class-based interface `CDC` and a function-based interface `cdc_cluster`.
|
|
27
|
+
|
|
28
|
+
### Class-based Usage
|
|
29
|
+
```python
|
|
30
|
+
from cdc_cluster import CDC
|
|
31
|
+
import numpy as np
|
|
32
|
+
import matplotlib.pyplot as plt
|
|
33
|
+
from sklearn.datasets import make_moons
|
|
34
|
+
|
|
35
|
+
# Generate sample data
|
|
36
|
+
X, _ = make_moons(n_samples=200, noise=0.05, random_state=42)
|
|
37
|
+
|
|
38
|
+
# Initialize and fit CDC
|
|
39
|
+
# n_neighbors: Number of nearest neighbors to consider (k_num)
|
|
40
|
+
# ratio: Ratio for determining the DCM threshold
|
|
41
|
+
cdc = CDC(n_neighbors=20, ratio=0.9)
|
|
42
|
+
cdc.fit(X)
|
|
43
|
+
|
|
44
|
+
# Get cluster labels
|
|
45
|
+
# Labels start from 0. Noisy samples are labeled as -1.
|
|
46
|
+
labels = cdc.labels_
|
|
47
|
+
|
|
48
|
+
# Plot result
|
|
49
|
+
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')
|
|
50
|
+
plt.title("CDC Clustering Result")
|
|
51
|
+
plt.show()
|
|
52
|
+
```
|
|
53
|
+
|
|
54
|
+
### Function-based Usage
|
|
55
|
+
```python
|
|
56
|
+
from cdc_cluster import cdc_cluster
|
|
57
|
+
from sklearn.datasets import make_blobs
|
|
58
|
+
|
|
59
|
+
X, _ = make_blobs(n_samples=200, centers=3, random_state=42)
|
|
60
|
+
|
|
61
|
+
# Compute clustering directly
|
|
62
|
+
# Returns an array of cluster labels
|
|
63
|
+
labels = cdc_cluster(X, n_neighbors=20, ratio=0.9)
|
|
64
|
+
|
|
65
|
+
print(f"Number of clusters: {len(set(labels)) - (1 if -1 in labels else 0)}")
|
|
66
|
+
```
|
|
67
|
+
|
|
68
|
+
# Citation Request:
|
|
69
|
+
Peng, D., Gui, Z.*, Wang, D. et al. Clustering by measuring local direction centrality for data with heterogeneous density and weak connectivity. Nat. Commun. 13, 5455 (2022).
|
|
70
|
+
https://www.nature.com/articles/s41467-022-33136-9
|
|
71
|
+
|
|
72
|
+
# License
|
|
73
|
+
|
|
74
|
+
This project is covered under the MIT License.
|
|
@@ -0,0 +1,262 @@
|
|
|
1
|
+
"""
|
|
2
|
+
Clustering by measuring local Direction Centrality (CDC).
|
|
3
|
+
"""
|
|
4
|
+
import math
|
|
5
|
+
import numpy as np
|
|
6
|
+
from scipy.special import gamma
|
|
7
|
+
from scipy.spatial import ConvexHull
|
|
8
|
+
from sklearn.base import BaseEstimator, ClusterMixin
|
|
9
|
+
from sklearn.neighbors import NearestNeighbors
|
|
10
|
+
from sklearn.utils.validation import check_array
|
|
11
|
+
|
|
12
|
+
def cdc_cluster(X, n_neighbors=20, ratio=0.9):
|
|
13
|
+
"""
|
|
14
|
+
Perform CDC clustering from vector array or distance matrix.
|
|
15
|
+
|
|
16
|
+
Parameters
|
|
17
|
+
----------
|
|
18
|
+
X : {array-like, sparse matrix} of shape (n_samples, n_features)
|
|
19
|
+
Training instances.
|
|
20
|
+
|
|
21
|
+
n_neighbors : int, default=20
|
|
22
|
+
Number of nearest neighbors to consider.
|
|
23
|
+
|
|
24
|
+
ratio : float, default=0.9
|
|
25
|
+
Ratio for determining the DCM threshold. Must be between 0 and 1.
|
|
26
|
+
|
|
27
|
+
Returns
|
|
28
|
+
-------
|
|
29
|
+
labels : ndarray of shape (n_samples,)
|
|
30
|
+
Cluster labels for each point. Noisy samples are given the label -1.
|
|
31
|
+
"""
|
|
32
|
+
X = check_array(X)
|
|
33
|
+
|
|
34
|
+
if n_neighbors <= 0:
|
|
35
|
+
raise ValueError("n_neighbors must be greater than 0")
|
|
36
|
+
if not (0 < ratio < 1):
|
|
37
|
+
raise ValueError("ratio must be between 0 and 1")
|
|
38
|
+
|
|
39
|
+
k_num = n_neighbors
|
|
40
|
+
num, d = X.shape
|
|
41
|
+
|
|
42
|
+
# Nearest Neighbors
|
|
43
|
+
# Note: We need k_num + 1 because the point itself is included
|
|
44
|
+
nbrs = NearestNeighbors(n_neighbors=k_num+1, algorithm='ball_tree').fit(X)
|
|
45
|
+
indices = nbrs.kneighbors(X, return_distance=False)
|
|
46
|
+
# Exclude the point itself (first column)
|
|
47
|
+
get_knn = indices[:, 1:k_num+1]
|
|
48
|
+
|
|
49
|
+
angle_var = np.zeros(num)
|
|
50
|
+
|
|
51
|
+
# Calculate DCM (Direction Centrality Metric)
|
|
52
|
+
if d == 2:
|
|
53
|
+
angle = np.zeros((num, k_num))
|
|
54
|
+
for i in range(num):
|
|
55
|
+
for j in range(k_num):
|
|
56
|
+
delta_x = X[get_knn[i, j], 0] - X[i, 0]
|
|
57
|
+
delta_y = X[get_knn[i, j], 1] - X[i, 1]
|
|
58
|
+
if delta_x == 0:
|
|
59
|
+
if delta_y == 0:
|
|
60
|
+
angle[i, j] = 0
|
|
61
|
+
elif delta_y > 0:
|
|
62
|
+
angle[i, j] = math.pi / 2
|
|
63
|
+
else:
|
|
64
|
+
angle[i, j] = 3 * math.pi / 2
|
|
65
|
+
elif delta_x > 0:
|
|
66
|
+
if math.atan(delta_y / delta_x) >= 0:
|
|
67
|
+
angle[i, j] = math.atan(delta_y / delta_x)
|
|
68
|
+
else:
|
|
69
|
+
angle[i, j] = 2 * math.pi + math.atan(delta_y / delta_x)
|
|
70
|
+
else:
|
|
71
|
+
angle[i, j] = math.pi + math.atan(delta_y / delta_x)
|
|
72
|
+
|
|
73
|
+
for i in range(num):
|
|
74
|
+
angle_order = sorted(angle[i, :])
|
|
75
|
+
|
|
76
|
+
for j in range(k_num - 1):
|
|
77
|
+
point_angle = angle_order[j + 1] - angle_order[j]
|
|
78
|
+
angle_var[i] = angle_var[i] + pow(point_angle - 2 * math.pi / k_num, 2)
|
|
79
|
+
|
|
80
|
+
point_angle = angle_order[0] - angle_order[k_num - 1] + 2 * math.pi
|
|
81
|
+
angle_var[i] = angle_var[i] + pow(point_angle - 2 * math.pi / k_num, 2)
|
|
82
|
+
angle_var[i] = angle_var[i] / k_num
|
|
83
|
+
|
|
84
|
+
angle_var = angle_var / ((k_num - 1) * 4 * pow(math.pi, 2) / pow(k_num, 2))
|
|
85
|
+
else:
|
|
86
|
+
for i in range(num):
|
|
87
|
+
try:
|
|
88
|
+
dif_x = X[get_knn[i], :] - X[i, :]
|
|
89
|
+
cov = np.dot(dif_x, dif_x.T)
|
|
90
|
+
if np.all(cov == 0):
|
|
91
|
+
map_x = dif_x
|
|
92
|
+
else:
|
|
93
|
+
map_x = np.linalg.inv(np.diag(np.sqrt(np.diag(cov)))) @ dif_x
|
|
94
|
+
|
|
95
|
+
hull = ConvexHull(map_x)
|
|
96
|
+
simplex_num = len(hull.simplices)
|
|
97
|
+
simplex_vol = np.zeros(simplex_num)
|
|
98
|
+
|
|
99
|
+
for j in range(simplex_num):
|
|
100
|
+
simplex_coord = map_x[hull.simplices[j], :]
|
|
101
|
+
simplex_vol[j] = np.sqrt(max(0, np.linalg.det(np.dot(simplex_coord, simplex_coord.T)))) / gamma(d-1)
|
|
102
|
+
|
|
103
|
+
angle_var[i] = np.var(simplex_vol)
|
|
104
|
+
|
|
105
|
+
except Exception:
|
|
106
|
+
angle_var[i] = 1
|
|
107
|
+
|
|
108
|
+
# Determine threshold
|
|
109
|
+
sort_dcm = sorted(angle_var)
|
|
110
|
+
idx = math.ceil(num * ratio)
|
|
111
|
+
if idx >= num:
|
|
112
|
+
idx = num - 1
|
|
113
|
+
T_DCM = sort_dcm[idx]
|
|
114
|
+
|
|
115
|
+
ind = np.zeros(num)
|
|
116
|
+
for i in range(num):
|
|
117
|
+
if angle_var[i] < T_DCM:
|
|
118
|
+
ind[i] = 1 # Internal point
|
|
119
|
+
|
|
120
|
+
near_dis = np.zeros(num)
|
|
121
|
+
for i in range(num):
|
|
122
|
+
knn_ind = ind[get_knn[i, :]]
|
|
123
|
+
if ind[i] == 1: # Internal
|
|
124
|
+
if 0 in knn_ind: # Has boundary neighbor
|
|
125
|
+
bdpts_ind = np.where(knn_ind == 0)[0]
|
|
126
|
+
bd_id = get_knn[i, bdpts_ind[0]]
|
|
127
|
+
near_dis[i] = math.sqrt(np.sum((X[i, :] - X[bd_id, :])**2))
|
|
128
|
+
else:
|
|
129
|
+
near_dis[i] = float("inf")
|
|
130
|
+
for j in range(num):
|
|
131
|
+
if ind[j] == 0:
|
|
132
|
+
temp_dis = math.sqrt(np.sum((X[i, :] - X[j, :])**2))
|
|
133
|
+
if temp_dis < near_dis[i]:
|
|
134
|
+
near_dis[i] = temp_dis
|
|
135
|
+
else: # Boundary
|
|
136
|
+
if 1 in knn_ind: # Has internal neighbor
|
|
137
|
+
bdpts_ind = np.where(knn_ind == 1)[0]
|
|
138
|
+
bd_id = get_knn[i, bdpts_ind[0]]
|
|
139
|
+
near_dis[i] = bd_id # Storing ID of nearest internal point
|
|
140
|
+
else:
|
|
141
|
+
mark_dis = float("inf")
|
|
142
|
+
for j in range(num):
|
|
143
|
+
if ind[j] == 1:
|
|
144
|
+
temp_dis = math.sqrt(np.sum((X[i, :] - X[j, :])**2))
|
|
145
|
+
if temp_dis < mark_dis:
|
|
146
|
+
mark_dis = temp_dis
|
|
147
|
+
near_dis[i] = j
|
|
148
|
+
|
|
149
|
+
# Clustering
|
|
150
|
+
cluster = np.zeros(num)
|
|
151
|
+
mark = 1
|
|
152
|
+
for i in range(num):
|
|
153
|
+
if ind[i] == 1 and cluster[i] == 0:
|
|
154
|
+
cluster[i] = mark
|
|
155
|
+
for j in range(num):
|
|
156
|
+
# Connectivity check
|
|
157
|
+
if ind[j] == 1:
|
|
158
|
+
dist = math.sqrt(np.sum((X[i, :] - X[j, :])**2))
|
|
159
|
+
if dist <= near_dis[i] + near_dis[j]:
|
|
160
|
+
if cluster[j] == 0:
|
|
161
|
+
cluster[j] = cluster[i]
|
|
162
|
+
else:
|
|
163
|
+
# Merge clusters
|
|
164
|
+
temp_cluster = cluster[j]
|
|
165
|
+
temp_ind = np.where(cluster == temp_cluster)
|
|
166
|
+
cluster[temp_ind] = cluster[i]
|
|
167
|
+
mark = mark + 1
|
|
168
|
+
|
|
169
|
+
# Assign boundary points
|
|
170
|
+
for i in range(num):
|
|
171
|
+
if ind[i] == 0:
|
|
172
|
+
cluster[i] = cluster[int(near_dis[i])]
|
|
173
|
+
|
|
174
|
+
# Remap labels: start from 0, use -1 for unassigned (noise)
|
|
175
|
+
# Original logic: 0 is unassigned, valid clusters >= 1
|
|
176
|
+
|
|
177
|
+
unique_labels = np.unique(cluster)
|
|
178
|
+
mapped_labels = np.full(num, -1, dtype=int)
|
|
179
|
+
|
|
180
|
+
current_label = 0
|
|
181
|
+
# Sort labels to ensure deterministic mapping (ignore 0)
|
|
182
|
+
sorted_labels = sorted([l for l in unique_labels if l != 0])
|
|
183
|
+
|
|
184
|
+
for old_label in sorted_labels:
|
|
185
|
+
mapped_labels[cluster == old_label] = current_label
|
|
186
|
+
current_label += 1
|
|
187
|
+
|
|
188
|
+
return mapped_labels
|
|
189
|
+
|
|
190
|
+
class CDC(BaseEstimator, ClusterMixin):
|
|
191
|
+
"""
|
|
192
|
+
Clustering by measuring local Direction Centrality (CDC).
|
|
193
|
+
|
|
194
|
+
Parameters
|
|
195
|
+
----------
|
|
196
|
+
n_neighbors : int, default=20
|
|
197
|
+
Number of nearest neighbors to consider.
|
|
198
|
+
|
|
199
|
+
ratio : float, default=0.9
|
|
200
|
+
Ratio for determining the DCM threshold. Must be between 0 and 1.
|
|
201
|
+
|
|
202
|
+
Attributes
|
|
203
|
+
----------
|
|
204
|
+
labels_ : ndarray of shape (n_samples,)
|
|
205
|
+
Cluster labels for each point. Noisy samples are given the label -1.
|
|
206
|
+
|
|
207
|
+
n_features_in_ : int
|
|
208
|
+
Number of features seen during :term:`fit`.
|
|
209
|
+
|
|
210
|
+
feature_names_in_ : ndarray of shape (n_features_in_,)
|
|
211
|
+
Names of features seen during :term:`fit`. Defined only when `X`
|
|
212
|
+
has feature names that are all strings.
|
|
213
|
+
|
|
214
|
+
References
|
|
215
|
+
----------
|
|
216
|
+
Peng, D., Gui, Z.*, Wang, D. et al. Clustering by measuring local
|
|
217
|
+
direction centrality for data with heterogeneous density and weak connectivity.
|
|
218
|
+
Nat. Commun. 13, 5455 (2022). https://www.nature.com/articles/s41467-022-33136-9
|
|
219
|
+
"""
|
|
220
|
+
def __init__(self, n_neighbors=20, ratio=0.9):
|
|
221
|
+
self.n_neighbors = n_neighbors
|
|
222
|
+
self.ratio = ratio
|
|
223
|
+
|
|
224
|
+
def fit(self, X, y=None):
|
|
225
|
+
"""Compute CDC clustering.
|
|
226
|
+
|
|
227
|
+
Parameters
|
|
228
|
+
----------
|
|
229
|
+
X : array-like of shape (n_samples, n_features)
|
|
230
|
+
Training instances.
|
|
231
|
+
|
|
232
|
+
y : Ignored
|
|
233
|
+
Not used, present here for API consistency by convention.
|
|
234
|
+
|
|
235
|
+
Returns
|
|
236
|
+
-------
|
|
237
|
+
self : object
|
|
238
|
+
Fitted estimator.
|
|
239
|
+
"""
|
|
240
|
+
X = check_array(X)
|
|
241
|
+
self.n_features_in_ = X.shape[1]
|
|
242
|
+
self.labels_ = cdc_cluster(X, n_neighbors=self.n_neighbors, ratio=self.ratio)
|
|
243
|
+
return self
|
|
244
|
+
|
|
245
|
+
def fit_predict(self, X, y=None):
|
|
246
|
+
"""Compute clusters and return cluster labels.
|
|
247
|
+
|
|
248
|
+
Parameters
|
|
249
|
+
----------
|
|
250
|
+
X : array-like of shape (n_samples, n_features)
|
|
251
|
+
Training instances.
|
|
252
|
+
|
|
253
|
+
y : Ignored
|
|
254
|
+
Not used, present here for API consistency by convention.
|
|
255
|
+
|
|
256
|
+
Returns
|
|
257
|
+
-------
|
|
258
|
+
labels : ndarray of shape (n_samples,)
|
|
259
|
+
Cluster labels.
|
|
260
|
+
"""
|
|
261
|
+
self.fit(X)
|
|
262
|
+
return self.labels_
|
|
@@ -1,6 +1,6 @@
|
|
|
1
1
|
Metadata-Version: 2.1
|
|
2
2
|
Name: cdc-cluster
|
|
3
|
-
Version: 0.
|
|
3
|
+
Version: 0.2.1
|
|
4
4
|
Summary: A novel Clustering algorithm by measuring Direction Centrality (CDC) locally. It adopts a density-independent metric based on the distribution of K-nearest neighbors (KNNs) to distinguish between internal and boundary points. The boundary points generate enclosed cages to bind the connections of internal points.
|
|
5
5
|
Author-email: pdh <pengdh@whu.edu.cn>
|
|
6
6
|
Project-URL: Homepage, https://github.com/ZPGuiGroupWhu/CDC-pkg
|
|
@@ -20,6 +20,7 @@ Classifier: Programming Language :: Python :: 3.11
|
|
|
20
20
|
Classifier: Programming Language :: Python :: 3.12
|
|
21
21
|
Requires-Python: >=3.8
|
|
22
22
|
Description-Content-Type: text/markdown
|
|
23
|
+
License-File: LICENSE
|
|
23
24
|
Requires-Dist: scikit-learn>=1.3.2
|
|
24
25
|
|
|
25
26
|
# Clustering by measuring local direction centrality for data with heterogeneous density and weak connectivity (CDC)
|
|
@@ -46,71 +47,49 @@ cd CDC-pkg
|
|
|
46
47
|
pip install -e .
|
|
47
48
|
```
|
|
48
49
|
|
|
49
|
-
#
|
|
50
|
-
The CDC algorithm
|
|
50
|
+
# Usage
|
|
51
|
+
The CDC algorithm is refactored to be a scikit-learn compatible estimator. It provides both a class-based interface `CDC` and a function-based interface `cdc_cluster`.
|
|
51
52
|
|
|
52
|
-
|
|
53
|
+
### Class-based Usage
|
|
53
54
|
```python
|
|
54
|
-
|
|
55
|
-
"""Clustering by measuring local Direction Centrality (CDC) algorithm.
|
|
56
|
-
|
|
57
|
-
This function implements the CDC clustering algorithm, which is a connectivity-based
|
|
58
|
-
clustering method that identifies boundary points using a directional centrality
|
|
59
|
-
metric (DCM) and connects internal points to generate cluster labels. DCM is defined
|
|
60
|
-
as angle variance in 2D space and simplex volume variance in higher dimensions.
|
|
61
|
-
|
|
62
|
-
The algorithm works in several steps:
|
|
63
|
-
1. For each point, find k-nearest neighbors
|
|
64
|
-
2. For each point, calculate its DCM
|
|
65
|
-
3. Identify boundary and internal points based on the DCM threshold
|
|
66
|
-
4. Calculate reachable distances of the internal points
|
|
67
|
-
5. Form clusters by connecting nearby internal points
|
|
68
|
-
6. Assign boundary points to nearest clusters
|
|
69
|
-
|
|
70
|
-
Args:
|
|
71
|
-
X (np.ndarray): Input data matrix of shape (n_samples, n_features).
|
|
72
|
-
Each row represents a data point and each column represents a feature.
|
|
73
|
-
k_num (int): Number of nearest neighbors to consider. Must be greater than 0.
|
|
74
|
-
This parameter controls the local neighborhood size.
|
|
75
|
-
ratio (float): Ratio for determining the DCM threshold. Must be between 0 and 1.
|
|
76
|
-
Lower values result in fewer internal points and more boundary points.
|
|
77
|
-
|
|
78
|
-
Returns:
|
|
79
|
-
np.ndarray: Cluster labels for each data point. Shape (n_samples,).
|
|
80
|
-
Labels are integers starting from 1, where points with the same label
|
|
81
|
-
belong to the same cluster.
|
|
82
|
-
|
|
83
|
-
Raises:
|
|
84
|
-
AssertionError: If k_num <= 0 or ratio is not in (0, 1).
|
|
85
|
-
ValueError: If X is not a 2D array or has insufficient data points.
|
|
86
|
-
|
|
87
|
-
Note:
|
|
88
|
-
- For 2D data, the algorithm uses angle variance between k-nearest neighbors
|
|
89
|
-
- For higher dimensional data, it uses convex hull simplex volume variance
|
|
90
|
-
- The algorithm automatically handles edge cases and numerical instabilities
|
|
91
|
-
"""
|
|
92
|
-
```
|
|
93
|
-
After installing the CDC library, you can use this function as follows:
|
|
94
|
-
```python
|
|
95
|
-
from cdc import cdc_cluster
|
|
55
|
+
from cdc_cluster import CDC
|
|
96
56
|
import numpy as np
|
|
97
|
-
import pandas as pd
|
|
98
57
|
import matplotlib.pyplot as plt
|
|
99
|
-
import
|
|
100
|
-
|
|
101
|
-
|
|
102
|
-
X =
|
|
103
|
-
|
|
104
|
-
|
|
105
|
-
|
|
106
|
-
|
|
107
|
-
|
|
108
|
-
|
|
109
|
-
|
|
110
|
-
|
|
111
|
-
|
|
58
|
+
from sklearn.datasets import make_moons
|
|
59
|
+
|
|
60
|
+
# Generate sample data
|
|
61
|
+
X, _ = make_moons(n_samples=200, noise=0.05, random_state=42)
|
|
62
|
+
|
|
63
|
+
# Initialize and fit CDC
|
|
64
|
+
# n_neighbors: Number of nearest neighbors to consider (k_num)
|
|
65
|
+
# ratio: Ratio for determining the DCM threshold
|
|
66
|
+
cdc = CDC(n_neighbors=20, ratio=0.9)
|
|
67
|
+
cdc.fit(X)
|
|
68
|
+
|
|
69
|
+
# Get cluster labels
|
|
70
|
+
# Labels start from 0. Noisy samples are labeled as -1.
|
|
71
|
+
labels = cdc.labels_
|
|
72
|
+
|
|
73
|
+
# Plot result
|
|
74
|
+
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')
|
|
75
|
+
plt.title("CDC Clustering Result")
|
|
112
76
|
plt.show()
|
|
113
77
|
```
|
|
78
|
+
|
|
79
|
+
### Function-based Usage
|
|
80
|
+
```python
|
|
81
|
+
from cdc_cluster import cdc_cluster
|
|
82
|
+
from sklearn.datasets import make_blobs
|
|
83
|
+
|
|
84
|
+
X, _ = make_blobs(n_samples=200, centers=3, random_state=42)
|
|
85
|
+
|
|
86
|
+
# Compute clustering directly
|
|
87
|
+
# Returns an array of cluster labels
|
|
88
|
+
labels = cdc_cluster(X, n_neighbors=20, ratio=0.9)
|
|
89
|
+
|
|
90
|
+
print(f"Number of clusters: {len(set(labels)) - (1 if -1 in labels else 0)}")
|
|
91
|
+
```
|
|
92
|
+
|
|
114
93
|
# Citation Request:
|
|
115
94
|
Peng, D., Gui, Z.*, Wang, D. et al. Clustering by measuring local direction centrality for data with heterogeneous density and weak connectivity. Nat. Commun. 13, 5455 (2022).
|
|
116
95
|
https://www.nature.com/articles/s41467-022-33136-9
|
|
@@ -1,9 +1,11 @@
|
|
|
1
|
+
LICENSE
|
|
1
2
|
README.md
|
|
2
3
|
pyproject.toml
|
|
3
|
-
|
|
4
|
+
cdc_cluster/__init__.py
|
|
5
|
+
cdc_cluster/_cdc.py
|
|
4
6
|
cdc_cluster.egg-info/PKG-INFO
|
|
5
7
|
cdc_cluster.egg-info/SOURCES.txt
|
|
6
8
|
cdc_cluster.egg-info/dependency_links.txt
|
|
7
9
|
cdc_cluster.egg-info/requires.txt
|
|
8
10
|
cdc_cluster.egg-info/top_level.txt
|
|
9
|
-
|
|
11
|
+
tests/test_cdc.py
|
|
@@ -0,0 +1 @@
|
|
|
1
|
+
cdc_cluster
|
|
@@ -1,6 +1,6 @@
|
|
|
1
1
|
[project]
|
|
2
2
|
name = "cdc-cluster"
|
|
3
|
-
version = "0.
|
|
3
|
+
version = "0.2.1"
|
|
4
4
|
description = "A novel Clustering algorithm by measuring Direction Centrality (CDC) locally. It adopts a density-independent metric based on the distribution of K-nearest neighbors (KNNs) to distinguish between internal and boundary points. The boundary points generate enclosed cages to bind the connections of internal points."
|
|
5
5
|
authors = [
|
|
6
6
|
{name = "pdh", email = "pengdh@whu.edu.cn"}
|
|
@@ -35,8 +35,16 @@ Repository = "https://github.com/ZPGuiGroupWhu/CDC-pkg.git"
|
|
|
35
35
|
"Bug Tracker" = "https://github.com/ZPGuiGroupWhu/CDC-pkg/issues"
|
|
36
36
|
|
|
37
37
|
[build-system]
|
|
38
|
-
requires = ["setuptools>=
|
|
38
|
+
requires = ["setuptools>=68.0", "wheel"]
|
|
39
39
|
build-backend = "setuptools.build_meta"
|
|
40
40
|
|
|
41
41
|
[tool.setuptools]
|
|
42
|
-
packages = ["
|
|
42
|
+
packages = ["cdc_cluster"]
|
|
43
|
+
|
|
44
|
+
[dependency-groups]
|
|
45
|
+
dev = [
|
|
46
|
+
"build>=1.2.2.post1",
|
|
47
|
+
"matplotlib>=3.7.5",
|
|
48
|
+
"pytest>=8.3.5",
|
|
49
|
+
"twine>=6.1.0",
|
|
50
|
+
]
|
|
@@ -0,0 +1,50 @@
|
|
|
1
|
+
import numpy as np
|
|
2
|
+
import pytest
|
|
3
|
+
from sklearn.datasets import make_blobs
|
|
4
|
+
from cdc_cluster import CDC, cdc_cluster
|
|
5
|
+
|
|
6
|
+
def test_cdc_class():
|
|
7
|
+
X, y = make_blobs(n_samples=100, centers=3, random_state=42)
|
|
8
|
+
cdc = CDC(n_neighbors=10, ratio=0.9)
|
|
9
|
+
cdc.fit(X)
|
|
10
|
+
assert hasattr(cdc, 'labels_')
|
|
11
|
+
|
|
12
|
+
# Check labels start from 0
|
|
13
|
+
unique_labels = np.unique(cdc.labels_)
|
|
14
|
+
# Filter out noise if any (-1)
|
|
15
|
+
valid_labels = unique_labels[unique_labels >= 0]
|
|
16
|
+
if len(valid_labels) > 0:
|
|
17
|
+
assert np.min(valid_labels) == 0
|
|
18
|
+
# Check consecutive integers (optional, but good practice if expected)
|
|
19
|
+
# CDC might produce gaps if not careful, but our remapping ensures consecutive 0..K-1
|
|
20
|
+
assert np.all(np.diff(sorted(valid_labels)) == 1)
|
|
21
|
+
|
|
22
|
+
# Check predictions match fit
|
|
23
|
+
labels = cdc.fit_predict(X)
|
|
24
|
+
assert np.array_equal(labels, cdc.labels_)
|
|
25
|
+
|
|
26
|
+
def test_cdc_function():
|
|
27
|
+
X, y = make_blobs(n_samples=100, centers=3, random_state=42)
|
|
28
|
+
labels = cdc_cluster(X, n_neighbors=10, ratio=0.9)
|
|
29
|
+
|
|
30
|
+
assert len(labels) == 100
|
|
31
|
+
unique_labels = np.unique(labels)
|
|
32
|
+
valid_labels = unique_labels[unique_labels >= 0]
|
|
33
|
+
|
|
34
|
+
if len(valid_labels) > 0:
|
|
35
|
+
assert np.min(valid_labels) == 0
|
|
36
|
+
|
|
37
|
+
def test_consistency():
|
|
38
|
+
X, y = make_blobs(n_samples=100, centers=3, random_state=42)
|
|
39
|
+
cdc = CDC(n_neighbors=10, ratio=0.9)
|
|
40
|
+
labels_class = cdc.fit_predict(X)
|
|
41
|
+
labels_func = cdc_cluster(X, n_neighbors=10, ratio=0.9)
|
|
42
|
+
|
|
43
|
+
assert np.array_equal(labels_class, labels_func)
|
|
44
|
+
|
|
45
|
+
def test_input_validation():
|
|
46
|
+
with pytest.raises(ValueError):
|
|
47
|
+
cdc_cluster(np.random.rand(10, 2), n_neighbors=-1)
|
|
48
|
+
|
|
49
|
+
with pytest.raises(ValueError):
|
|
50
|
+
cdc_cluster(np.random.rand(10, 2), ratio=1.5)
|
cdc_cluster-0.1.1/README.md
DELETED
|
@@ -1,96 +0,0 @@
|
|
|
1
|
-
# Clustering by measuring local direction centrality for data with heterogeneous density and weak connectivity (CDC)
|
|
2
|
-
|
|
3
|
-
|
|
4
|
-
We propose a novel Clustering algorithm by measuring Direction Centrality (CDC) locally. It adopts a density-independent metric based on the distribution of K-nearest neighbors (KNNs) to distinguish between internal and boundary points. The boundary points generate enclosed cages to bind the connections of internal points, thereby preventing cross-cluster connections and separating weakly-connected clusters. We present an interactive ***Demo*** and a brief introduction to the algorithm at ***https://zpguigroupwhu.github.io/CDC-Introduction-Website/***, and develop a CDC toolkit at ***https://github.com/ZPGuiGroupWhu/ClusteringDirectionCentrality*** This paper has been published in ***Nature Communications***, and more details can be seen https://www.nature.com/articles/s41467-022-33136-9.
|
|
5
|
-
|
|
6
|
-

|
|
7
|
-
|
|
8
|
-
# Installation
|
|
9
|
-
Supported `python` versions are `3.8` and above.
|
|
10
|
-
|
|
11
|
-
This project has been uploaded to [PyPI](https://pypi.org/project/cdc-cluster/), supporting direct download and installation from pypi
|
|
12
|
-
|
|
13
|
-
```
|
|
14
|
-
pip install cdc-cluster
|
|
15
|
-
```
|
|
16
|
-
|
|
17
|
-
## Manual Installation
|
|
18
|
-
|
|
19
|
-
```
|
|
20
|
-
git clone https://github.com/ZPGuiGroupWhu/CDC-pkg.git
|
|
21
|
-
cd CDC-pkg
|
|
22
|
-
pip install -e .
|
|
23
|
-
```
|
|
24
|
-
|
|
25
|
-
# How To Run
|
|
26
|
-
The CDC algorithm package provides the `cdc_cluster` function for clustering.
|
|
27
|
-
|
|
28
|
-
The description of the hyperparameters for user configuration are presented as follows
|
|
29
|
-
```python
|
|
30
|
-
def cdc_cluster(X: np.ndarray, k_num: int, ratio: float) -> np.ndarray:
|
|
31
|
-
"""Clustering by measuring local Direction Centrality (CDC) algorithm.
|
|
32
|
-
|
|
33
|
-
This function implements the CDC clustering algorithm, which is a connectivity-based
|
|
34
|
-
clustering method that identifies boundary points using a directional centrality
|
|
35
|
-
metric (DCM) and connects internal points to generate cluster labels. DCM is defined
|
|
36
|
-
as angle variance in 2D space and simplex volume variance in higher dimensions.
|
|
37
|
-
|
|
38
|
-
The algorithm works in several steps:
|
|
39
|
-
1. For each point, find k-nearest neighbors
|
|
40
|
-
2. For each point, calculate its DCM
|
|
41
|
-
3. Identify boundary and internal points based on the DCM threshold
|
|
42
|
-
4. Calculate reachable distances of the internal points
|
|
43
|
-
5. Form clusters by connecting nearby internal points
|
|
44
|
-
6. Assign boundary points to nearest clusters
|
|
45
|
-
|
|
46
|
-
Args:
|
|
47
|
-
X (np.ndarray): Input data matrix of shape (n_samples, n_features).
|
|
48
|
-
Each row represents a data point and each column represents a feature.
|
|
49
|
-
k_num (int): Number of nearest neighbors to consider. Must be greater than 0.
|
|
50
|
-
This parameter controls the local neighborhood size.
|
|
51
|
-
ratio (float): Ratio for determining the DCM threshold. Must be between 0 and 1.
|
|
52
|
-
Lower values result in fewer internal points and more boundary points.
|
|
53
|
-
|
|
54
|
-
Returns:
|
|
55
|
-
np.ndarray: Cluster labels for each data point. Shape (n_samples,).
|
|
56
|
-
Labels are integers starting from 1, where points with the same label
|
|
57
|
-
belong to the same cluster.
|
|
58
|
-
|
|
59
|
-
Raises:
|
|
60
|
-
AssertionError: If k_num <= 0 or ratio is not in (0, 1).
|
|
61
|
-
ValueError: If X is not a 2D array or has insufficient data points.
|
|
62
|
-
|
|
63
|
-
Note:
|
|
64
|
-
- For 2D data, the algorithm uses angle variance between k-nearest neighbors
|
|
65
|
-
- For higher dimensional data, it uses convex hull simplex volume variance
|
|
66
|
-
- The algorithm automatically handles edge cases and numerical instabilities
|
|
67
|
-
"""
|
|
68
|
-
```
|
|
69
|
-
After installing the CDC library, you can use this function as follows:
|
|
70
|
-
```python
|
|
71
|
-
from cdc import cdc_cluster
|
|
72
|
-
import numpy as np
|
|
73
|
-
import pandas as pd
|
|
74
|
-
import matplotlib.pyplot as plt
|
|
75
|
-
import time
|
|
76
|
-
# DS1.txt link: https://github.com/ZPGuiGroupWhu/ClusteringDirectionCentrality/blob/master/Toolkit/Python/DS1.txt
|
|
77
|
-
raw_data = pd.read_table('DS1.txt', header=None)
|
|
78
|
-
X = np.array(raw_data)
|
|
79
|
-
[n, d] = X.shape
|
|
80
|
-
data = X[:, :d-1]
|
|
81
|
-
ref = X[:, d-1]
|
|
82
|
-
time_start = time.time()
|
|
83
|
-
res = cdc_cluster(X=data, k_num=30, ratio=0.72)
|
|
84
|
-
time_end = time.time()
|
|
85
|
-
print(time_end-time_start)
|
|
86
|
-
|
|
87
|
-
plt.scatter(data[:, 0], data[:, 1], c=res, s=10, cmap='hsv', marker='o')
|
|
88
|
-
plt.show()
|
|
89
|
-
```
|
|
90
|
-
# Citation Request:
|
|
91
|
-
Peng, D., Gui, Z.*, Wang, D. et al. Clustering by measuring local direction centrality for data with heterogeneous density and weak connectivity. Nat. Commun. 13, 5455 (2022).
|
|
92
|
-
https://www.nature.com/articles/s41467-022-33136-9
|
|
93
|
-
|
|
94
|
-
# License
|
|
95
|
-
|
|
96
|
-
This project is covered under the MIT License.
|
|
@@ -1,193 +0,0 @@
|
|
|
1
|
-
import math
|
|
2
|
-
import numpy as np
|
|
3
|
-
from sklearn.neighbors import NearestNeighbors
|
|
4
|
-
from scipy.special import gamma
|
|
5
|
-
from scipy.spatial import ConvexHull
|
|
6
|
-
|
|
7
|
-
__all__ = ['cdc_cluster']
|
|
8
|
-
|
|
9
|
-
def cdc_cluster(X: np.ndarray, k_num: int, ratio: float) -> np.ndarray:
|
|
10
|
-
"""Clustering by measuring local Direction Centrality (CDC) algorithm.
|
|
11
|
-
|
|
12
|
-
This function implements the CDC clustering algorithm, which is a connectivity-based
|
|
13
|
-
clustering method that identifies boundary points using a directional centrality
|
|
14
|
-
metric (DCM) and connects internal points to generate cluster labels. DCM is defined
|
|
15
|
-
as angle variance in 2D space and simplex volume variance in higher dimensions.
|
|
16
|
-
|
|
17
|
-
paper reference: Peng, D., Gui, Z.*, Wang, D. et al. Clustering by measuring local
|
|
18
|
-
direction centrality for data with heterogeneous density and weak connectivity.
|
|
19
|
-
Nat. Commun. 13, 5455 (2022). https://www.nature.com/articles/s41467-022-33136-9
|
|
20
|
-
|
|
21
|
-
The algorithm works in several steps:
|
|
22
|
-
1. For each point, find k-nearest neighbors
|
|
23
|
-
2. For each point, calculate its DCM
|
|
24
|
-
3. Identify boundary and internal points based on the DCM threshold
|
|
25
|
-
4. Calculate reachable distances of the internal points
|
|
26
|
-
5. Form clusters by connecting nearby internal points
|
|
27
|
-
6. Assign boundary points to nearest clusters
|
|
28
|
-
|
|
29
|
-
Args:
|
|
30
|
-
X (np.ndarray): Input data matrix of shape (n_samples, n_features).
|
|
31
|
-
Each row represents a data point and each column represents a feature.
|
|
32
|
-
k_num (int): Number of nearest neighbors to consider. Must be greater than 0.
|
|
33
|
-
This parameter controls the local neighborhood size.
|
|
34
|
-
ratio (float): Ratio for determining the DCM threshold. Must be between 0 and 1.
|
|
35
|
-
Lower values result in fewer internal points and more boundary points.
|
|
36
|
-
|
|
37
|
-
|
|
38
|
-
Returns:
|
|
39
|
-
np.ndarray: Cluster labels for each data point. Shape (n_samples,).
|
|
40
|
-
Labels are integers starting from 1, where points with the same label
|
|
41
|
-
belong to the same cluster.
|
|
42
|
-
|
|
43
|
-
Raises:
|
|
44
|
-
AssertionError: If k_num <= 0 or ratio is not in (0, 1).
|
|
45
|
-
ValueError: If X is not a 2D array or has insufficient data points.
|
|
46
|
-
|
|
47
|
-
Example:
|
|
48
|
-
>>> import numpy as np
|
|
49
|
-
>>> from CDC import cdc_cluster
|
|
50
|
-
>>>
|
|
51
|
-
>>> # Generate sample 2D data
|
|
52
|
-
>>> X = np.random.rand(100, 2)
|
|
53
|
-
>>>
|
|
54
|
-
>>> # Apply CDC clustering
|
|
55
|
-
>>> labels = cdc_cluster(X=X, k_num=20, ratio=0.9)
|
|
56
|
-
>>>
|
|
57
|
-
>>> # Get number of clusters
|
|
58
|
-
>>> n_clusters = len(np.unique(labels))
|
|
59
|
-
>>> print(f"Number of clusters: {n_clusters}")
|
|
60
|
-
|
|
61
|
-
Note:
|
|
62
|
-
- For 2D data, the algorithm uses angle variance between k-nearest neighbors
|
|
63
|
-
- For higher dimensional data, it uses convex hull simplex volume variance
|
|
64
|
-
- The algorithm automatically handles edge cases and numerical instabilities
|
|
65
|
-
"""
|
|
66
|
-
assert k_num > 0, "k_num must be greater than 0"
|
|
67
|
-
assert 0 < ratio < 1, "ratio must be between 0 and 1"
|
|
68
|
-
|
|
69
|
-
[num, d] = X.shape
|
|
70
|
-
nbrs = NearestNeighbors(n_neighbors=k_num+1, algorithm='ball_tree').fit(X)
|
|
71
|
-
indices = nbrs.kneighbors(X, return_distance=False)
|
|
72
|
-
get_knn = indices[:, 1:k_num+1]
|
|
73
|
-
|
|
74
|
-
angle_var = np.zeros(num)
|
|
75
|
-
if (d == 2):
|
|
76
|
-
angle = np.zeros((num, k_num))
|
|
77
|
-
for i in range(num):
|
|
78
|
-
for j in range(k_num):
|
|
79
|
-
delta_x = X[get_knn[i, j], 0] - X[i, 0]
|
|
80
|
-
delta_y = X[get_knn[i, j], 1] - X[i, 1]
|
|
81
|
-
if delta_x == 0:
|
|
82
|
-
if delta_y == 0:
|
|
83
|
-
angle[i, j] = 0
|
|
84
|
-
elif delta_y > 0:
|
|
85
|
-
angle[i, j] = math.pi / 2
|
|
86
|
-
else:
|
|
87
|
-
angle[i, j] = 3 * math.pi / 2
|
|
88
|
-
elif delta_x > 0:
|
|
89
|
-
if math.atan(delta_y / delta_x) >= 0:
|
|
90
|
-
angle[i, j] = math.atan(delta_y / delta_x)
|
|
91
|
-
else:
|
|
92
|
-
angle[i, j] = 2 * math.pi + math.atan(delta_y / delta_x)
|
|
93
|
-
else:
|
|
94
|
-
angle[i, j] = math.pi + math.atan(delta_y / delta_x)
|
|
95
|
-
|
|
96
|
-
for i in range(num):
|
|
97
|
-
angle_order = sorted(angle[i, :])
|
|
98
|
-
|
|
99
|
-
for j in range(k_num - 1):
|
|
100
|
-
point_angle = angle_order[j + 1] - angle_order[j]
|
|
101
|
-
angle_var[i] = angle_var[i] + pow(point_angle - 2 * math.pi / k_num, 2)
|
|
102
|
-
|
|
103
|
-
point_angle = angle_order[0] - angle_order[k_num - 1] + 2 * math.pi
|
|
104
|
-
angle_var[i] = angle_var[i] + pow(point_angle - 2 * math.pi / k_num, 2)
|
|
105
|
-
angle_var[i] = angle_var[i] / k_num
|
|
106
|
-
|
|
107
|
-
angle_var = angle_var / ((k_num - 1) * 4 * pow(math.pi, 2) / pow(k_num, 2))
|
|
108
|
-
else:
|
|
109
|
-
for i in range(num):
|
|
110
|
-
try:
|
|
111
|
-
dif_x = X[get_knn[i], :] - X[i, :]
|
|
112
|
-
map_x = np.linalg.inv(np.diag(np.sqrt(np.diag(np.dot(dif_x, dif_x.T))))) @ dif_x
|
|
113
|
-
hull = ConvexHull(map_x)
|
|
114
|
-
simplex_num = len(hull.simplices)
|
|
115
|
-
simplex_vol = np.zeros(simplex_num)
|
|
116
|
-
|
|
117
|
-
for j in range(simplex_num):
|
|
118
|
-
simplex_coord = map_x[hull.simplices[j], :]
|
|
119
|
-
simplex_vol[j] = np.sqrt(max(0, np.linalg.det(np.dot(simplex_coord, simplex_coord.T)))) / gamma(d-1)
|
|
120
|
-
|
|
121
|
-
angle_var[i] = np.var(simplex_vol)
|
|
122
|
-
|
|
123
|
-
except Exception as e:
|
|
124
|
-
angle_var[i] = 1
|
|
125
|
-
|
|
126
|
-
sort_dcm = sorted(angle_var)
|
|
127
|
-
T_DCM = sort_dcm[math.ceil(num*ratio)]
|
|
128
|
-
ind = np.zeros(num)
|
|
129
|
-
for i in range(num):
|
|
130
|
-
if angle_var[i] < T_DCM:
|
|
131
|
-
ind[i] = 1
|
|
132
|
-
|
|
133
|
-
near_dis = np.zeros(num)
|
|
134
|
-
for i in range(num):
|
|
135
|
-
knn_ind = ind[get_knn[i, :]]
|
|
136
|
-
if ind[i] == 1:
|
|
137
|
-
if 0 in knn_ind:
|
|
138
|
-
bdpts_ind = np.where(knn_ind == 0)
|
|
139
|
-
bd_id = get_knn[i, bdpts_ind[0][0]]
|
|
140
|
-
near_dis[i] = math.sqrt(sum(pow((X[i, :] - X[bd_id, :]), 2)))
|
|
141
|
-
else:
|
|
142
|
-
near_dis[i] = float("inf")
|
|
143
|
-
for j in range(num):
|
|
144
|
-
if ind[j] == 0:
|
|
145
|
-
temp_dis = math.sqrt(sum(pow((X[i, :] - X[j, :]), 2)))
|
|
146
|
-
if temp_dis < near_dis[i]:
|
|
147
|
-
near_dis[i] = temp_dis
|
|
148
|
-
else:
|
|
149
|
-
if 1 in knn_ind:
|
|
150
|
-
bdpts_ind = np.where(knn_ind == 1)
|
|
151
|
-
bd_id = get_knn[i, bdpts_ind[0][0]]
|
|
152
|
-
near_dis[i] = bd_id
|
|
153
|
-
else:
|
|
154
|
-
mark_dis = float("inf")
|
|
155
|
-
for j in range(num):
|
|
156
|
-
if ind[j] == 1:
|
|
157
|
-
temp_dis = math.sqrt(sum(pow((X[i, :] - X[j, :]), 2)))
|
|
158
|
-
if temp_dis < mark_dis:
|
|
159
|
-
mark_dis = temp_dis
|
|
160
|
-
near_dis[i] = j
|
|
161
|
-
|
|
162
|
-
cluster = np.zeros(num)
|
|
163
|
-
mark = 1
|
|
164
|
-
for i in range(num):
|
|
165
|
-
if ind[i] == 1 and cluster[i] == 0:
|
|
166
|
-
cluster[i] = mark
|
|
167
|
-
for j in range(num):
|
|
168
|
-
if ind[j] == 1 and math.sqrt(sum(pow((X[i, :] - X[j, :]), 2))) <= near_dis[i] + near_dis[j]:
|
|
169
|
-
if cluster[j] == 0:
|
|
170
|
-
cluster[j] = cluster[i]
|
|
171
|
-
else:
|
|
172
|
-
temp_cluster = cluster[j]
|
|
173
|
-
temp_ind = np.where(cluster == temp_cluster)
|
|
174
|
-
cluster[temp_ind] = cluster[i]
|
|
175
|
-
|
|
176
|
-
mark = mark + 1
|
|
177
|
-
|
|
178
|
-
for i in range(num):
|
|
179
|
-
if ind[i] == 0:
|
|
180
|
-
cluster[i] = cluster[int(near_dis[i])]
|
|
181
|
-
|
|
182
|
-
mark = 1
|
|
183
|
-
storage = np.zeros(num)
|
|
184
|
-
for i in range(num):
|
|
185
|
-
if cluster[i] in storage:
|
|
186
|
-
temp_ind = np.where(storage == cluster[i])
|
|
187
|
-
cluster[i] = cluster[temp_ind[0][0]]
|
|
188
|
-
else:
|
|
189
|
-
storage[i] = cluster[i]
|
|
190
|
-
cluster[i] = mark
|
|
191
|
-
mark = mark + 1
|
|
192
|
-
|
|
193
|
-
return cluster
|
|
@@ -1 +0,0 @@
|
|
|
1
|
-
cdc
|
cdc_cluster-0.1.1/test/test1.py
DELETED
|
File without changes
|
|
File without changes
|
|
File without changes
|