mhl 0.1.0 → 0.2.0
This diff represents the content of publicly available package versions that have been released to one of the supported registries. The information contained in this diff is provided for informational purposes only and reflects changes between package versions as they appear in their respective public registries.
- checksums.yaml +4 -4
- data/README.md +203 -12
- data/lib/mhl/charged_swarm.rb +31 -19
- data/lib/mhl/generic_particle.rb +0 -28
- data/lib/mhl/generic_swarm.rb +12 -10
- data/lib/mhl/genetic_algorithm_solver.rb +1 -2
- data/lib/mhl/multiswarm_qpso_solver.rb +62 -24
- data/lib/mhl/particle.rb +47 -12
- data/lib/mhl/particle_swarm_optimization_solver.rb +67 -33
- data/lib/mhl/pso_swarm.rb +11 -14
- data/lib/mhl/qpso_swarm.rb +23 -12
- data/lib/mhl/quantum_particle.rb +29 -10
- data/lib/mhl/quantum_particle_swarm_optimization_solver.rb +35 -21
- data/lib/mhl/version.rb +1 -1
- data/mhl.gemspec +2 -3
- data/test/mhl/multiswarm_qpso_solver_test.rb +5 -4
- data/test/mhl/particle_swarm_optimization_solver_test.rb +5 -4
- data/test/mhl/quantum_particle_swarm_optimization_solver_test.rb +5 -3
- metadata +18 -32
checksums.yaml
CHANGED
|
@@ -1,7 +1,7 @@
|
|
|
1
1
|
---
|
|
2
2
|
SHA1:
|
|
3
|
-
metadata.gz:
|
|
4
|
-
data.tar.gz:
|
|
3
|
+
metadata.gz: 3e0490b924de2e42d7fd0935673abd7d232b07ed
|
|
4
|
+
data.tar.gz: 51076e97078fc49710f9b6d86dc236e09cac5d99
|
|
5
5
|
SHA512:
|
|
6
|
-
metadata.gz:
|
|
7
|
-
data.tar.gz:
|
|
6
|
+
metadata.gz: a1aac62bdff38e7c43d0bd58c06703ccf0df63a365b9c9e004b8f1a2a8f2cba59d2772a6e37c2dbba2c928e3ce5dffad6fd8b7c258c40979789a09217fdde090
|
|
7
|
+
data.tar.gz: 383e9ce734b17fbb47f843ff91e487b53dfed05a1df65bb70a09678b61eb98948b542eff2f3b45f9435d030ae5f7cbc816dc12ac2ba4447ad86e704469a1db97
|
data/README.md
CHANGED
|
@@ -1,10 +1,33 @@
|
|
|
1
|
-
#ruby-mhl
|
|
1
|
+
# ruby-mhl - A Ruby metaheuristics library
|
|
2
2
|
|
|
3
|
-
|
|
3
|
+
ruby-mhl is a scientific library that provides a fairly large array of advanced
|
|
4
|
+
computational intelligence methods for continuous optimization solutions.
|
|
5
|
+
|
|
6
|
+
More specifically, ruby-mhl currently supports several implementations of
|
|
7
|
+
Genetic Algorithms (bitstring and integer vector genotype representations) and
|
|
8
|
+
Particle Swarm Optimization (constrained PSO, quantum-inspired PSO, and a
|
|
9
|
+
multi-swarm version of quantum-inspired PSO), extended with adaptation
|
|
10
|
+
mechanisms to provide support for dynamic optimization problems.
|
|
11
|
+
|
|
12
|
+
ruby-mhl was designed for _high duty_ target functions, whose evaluation
|
|
13
|
+
typically involves one or more simulation runs, possibly defined on very
|
|
14
|
+
complex domains (or search spaces), and implemented in JRuby for performance
|
|
15
|
+
reasons. To this end, ruby-mhl automatically takes advantage of the parallelism
|
|
16
|
+
provided by the processor.
|
|
4
17
|
|
|
5
18
|
|
|
6
19
|
## Installation
|
|
7
20
|
|
|
21
|
+
To install ruby-mhl you first have to install Java and JRuby. This is a system
|
|
22
|
+
dependent step, so I won't show you how to do it. However, if you are on Linux
|
|
23
|
+
or OS X I recommend you to use [rbenv](https://github.com/rbenv/rbenv) to
|
|
24
|
+
install and manage your Ruby installations.
|
|
25
|
+
|
|
26
|
+
Once you have JRuby installed, you need to install bundler:
|
|
27
|
+
|
|
28
|
+
gem install bundler
|
|
29
|
+
|
|
30
|
+
|
|
8
31
|
### Stable version
|
|
9
32
|
|
|
10
33
|
You can get the stable version of ruby-mhl by installing the mhl gem from
|
|
@@ -12,6 +35,16 @@ RubyGems:
|
|
|
12
35
|
|
|
13
36
|
gem install mhl
|
|
14
37
|
|
|
38
|
+
or by adding:
|
|
39
|
+
|
|
40
|
+
```ruby
|
|
41
|
+
gem 'mhl'
|
|
42
|
+
```
|
|
43
|
+
|
|
44
|
+
to your application's Gemfile and running:
|
|
45
|
+
|
|
46
|
+
bundle install
|
|
47
|
+
|
|
15
48
|
### Development version
|
|
16
49
|
|
|
17
50
|
If you want to try the development version of ruby-mhl, instead, just place
|
|
@@ -26,46 +59,204 @@ in your Gemfile and run:
|
|
|
26
59
|
bundle install
|
|
27
60
|
|
|
28
61
|
|
|
29
|
-
##
|
|
62
|
+
## Genetic Algorithm (GA)
|
|
63
|
+
|
|
64
|
+
ruby-mhl provides a GA solver capable of working with either the traditional
|
|
65
|
+
bitstring chromosome representation or a integer vector representation variant.
|
|
66
|
+
|
|
67
|
+
#### Example: Solving the parabola function with a integer vector GA
|
|
30
68
|
|
|
31
69
|
Here is an example demonstrating how to find the argument that minimizes the
|
|
32
|
-
2-dimension parabola
|
|
70
|
+
2-dimension parabola _f(x) = x<sub>1</sub><sup>2</sup> +
|
|
71
|
+
x<sub>2</sub><sup>2</sup>_ equation with a genetic algorithm:
|
|
33
72
|
|
|
34
73
|
```ruby
|
|
35
74
|
require 'mhl'
|
|
36
75
|
|
|
37
76
|
solver = MHL::GeneticAlgorithmSolver.new(
|
|
38
|
-
:population_size =>
|
|
77
|
+
:population_size => 80,
|
|
39
78
|
:genotype_space_type => :integer,
|
|
40
79
|
:mutation_probability => 0.5,
|
|
41
80
|
:recombination_probability => 0.5,
|
|
42
81
|
:genotype_space_conf => {
|
|
43
82
|
:dimensions => 2,
|
|
44
83
|
:recombination_type => :intermediate,
|
|
45
|
-
:random_func => lambda { Array.new(2) { rand(
|
|
84
|
+
:random_func => lambda { Array.new(2) { rand(100) } }
|
|
46
85
|
},
|
|
47
86
|
:exit_condition => lambda {|generation,best| best[:fitness] == 0}
|
|
48
87
|
)
|
|
49
88
|
solver.solve(Proc.new{|x| -(x[0] ** 2 + x[1] ** 2) })
|
|
50
89
|
```
|
|
51
90
|
|
|
52
|
-
|
|
91
|
+
|
|
92
|
+
## Particle Swarm Optimization (PSO)
|
|
93
|
+
|
|
94
|
+
ruby-mhl implements the constrained version of PSO, defined by equation 4.30 of
|
|
95
|
+
[SUN11], which we report here for full clarity. The velocity and position
|
|
96
|
+
update equation for particle _i_ are:
|
|
97
|
+
|
|
98
|
+
<!--
|
|
99
|
+
```latex
|
|
100
|
+
\begin{aligned}
|
|
101
|
+
V_{i,j}(t+1) =& \; \chi [ V_{i,j}(t) + \\
|
|
102
|
+
& \quad C_1 * r_{i,j}(t) * (P_{i,j}(t) - X_{i,j}(t)) + \\
|
|
103
|
+
& \quad C_2 * R_{i,j}(t) * (G_j(t) - X_{i,j}(t)) ] \\
|
|
104
|
+
X_{i,j}(t+1) =& \; X_{i,j}(t) + V_{i,j}(t+1)
|
|
105
|
+
\end{aligned}
|
|
106
|
+
```
|
|
107
|
+
-->
|
|
108
|
+
|
|
109
|
+
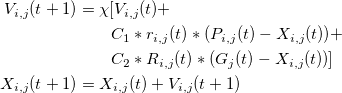
|
|
110
|
+
|
|
111
|
+
In which _X<sub>i</sub>(t) = (X<sub>i,1</sub>(t), ..., X<sub>i,N</sub>(t))_ is
|
|
112
|
+
the particle location, whose components _X<sub>i,j</sub>(t)_ represent the
|
|
113
|
+
decision variables of the problem; _V<sub>i</sub>(t) = (V<sub>i,1</sub>(t),
|
|
114
|
+
..., V<sub>i,N</sub>(t))_ is a velocity vector which captures the movement of
|
|
115
|
+
the particle; _P<sub>i</sub>(t) = (P<sub>i,1</sub>(t), ...,
|
|
116
|
+
P<sub>i,N</sub>(t))_ is a _particle attractor_ representing the 'highest'
|
|
117
|
+
(best) position that the particle has encountered so far; _G(t)_ is the _swarm
|
|
118
|
+
attractor_, representing the 'highest' (best) position that the entire swarm
|
|
119
|
+
has encountered so far; _r<sub>i,j</sub>(t)_ and _R<sub>i,j</sub>(t)_ are
|
|
120
|
+
random sequences uniformly sampled in the (0,1) interval; and _C<sub>1</sub>_
|
|
121
|
+
and _C<sub>2</sub>_ are constants.
|
|
122
|
+
|
|
123
|
+
Note that, in order to guarantee convergence, we must have:
|
|
124
|
+
|
|
125
|
+
<!--
|
|
126
|
+
```latex
|
|
127
|
+
\begin{aligned}
|
|
128
|
+
\phi =& C_1 + C_2 > 4\\
|
|
129
|
+
\chi =& \frac{2}{\lvert 2-\phi-\sqrt{\phi^2-4\phi} \rvert}
|
|
130
|
+
\end{aligned}
|
|
131
|
+
```
|
|
132
|
+
-->
|
|
133
|
+
|
|
134
|
+
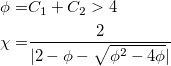
|
|
135
|
+
|
|
136
|
+
As a result, by default ruby-mhl sets _C<sub>1</sub> = C<sub>2</sub> = 2.05_
|
|
137
|
+
and calculates χ accordingly (approximately 0.72984), which is considered
|
|
138
|
+
the best practice [BLACKWELL04]. For more information about this (much more
|
|
139
|
+
than you'll ever want to know, believe me) please refer to [CLERC02].
|
|
140
|
+
|
|
141
|
+
#### Example: Solving the parabola function with PSO
|
|
142
|
+
|
|
143
|
+
Here is an example demonstrating how to find the argument that minimizes the
|
|
144
|
+
2-dimension parabola _f(x) = x<sub>1</sub><sup>2</sup> +
|
|
145
|
+
x<sub>2</sub><sup>2</sup>_ equation with PSO:
|
|
53
146
|
|
|
54
147
|
```ruby
|
|
55
148
|
require 'mhl'
|
|
56
149
|
|
|
57
150
|
solver = MHL::ParticleSwarmOptimizationSolver.new(
|
|
58
|
-
:swarm_size
|
|
59
|
-
:
|
|
60
|
-
|
|
61
|
-
|
|
151
|
+
:swarm_size => 40, # 40 is the default swarm size
|
|
152
|
+
:constraints => {
|
|
153
|
+
:min => [ -100, -100 ],
|
|
154
|
+
:max => [ 100, 100 ],
|
|
155
|
+
},
|
|
156
|
+
:exit_condition => lambda {|iteration,best| best[:height].abs < 0.001 },
|
|
62
157
|
)
|
|
63
158
|
solver.solve(Proc.new{|x| -(x[0] ** 2 + x[1] ** 2) })
|
|
64
159
|
```
|
|
65
160
|
|
|
66
|
-
|
|
161
|
+
|
|
162
|
+
## Quantum-Inspired Particle Swarm Optimization (QPSO)
|
|
163
|
+
|
|
164
|
+
Quantum-inspired PSO is another particularly interesting PSO variant. It aims
|
|
165
|
+
at simulating interactions between a group of humans by borrowing concepts
|
|
166
|
+
from (the uncertainty typical of) quantum mechanics.
|
|
167
|
+
|
|
168
|
+
ruby-mhl implements the Quantum-inspired version of PSO (QPSO), Type 2, as
|
|
169
|
+
defined by equation 4.82 of [SUN11], which we report here for full clarity.
|
|
170
|
+
|
|
171
|
+
<!--
|
|
172
|
+
```latex
|
|
173
|
+
\begin{equation}
|
|
174
|
+
\begin{aligned}
|
|
175
|
+
C_j(t) &= \frac{1}{M} \sum_{i=1}^{M} P_{i,j}(t) \\
|
|
176
|
+
p_{i,j}(t) &= \phi_{i,j}(t) P_{i,j}(t) + (1-\phi_{i,j}(t)) G_j(t) \\
|
|
177
|
+
X_{i,j}(t+1) &= p_{i,j}(t) + \alpha \lvert X_{i,j}(t) - C_j(t) \rvert \ln \frac{1}{u_{i,j}(t+1)}
|
|
178
|
+
\end{aligned}
|
|
179
|
+
\end{equation}
|
|
180
|
+
```
|
|
181
|
+
-->
|
|
182
|
+
|
|
183
|
+
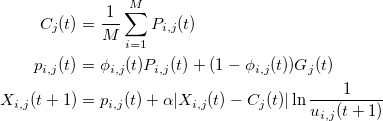
|
|
184
|
+
|
|
185
|
+
where _P<sub>i</sub>(t)_ is the personal best of particle _i_; _C(t)_ is
|
|
186
|
+
the mean of the personal bests of all the particles in the swarm; _G(t)_ is the
|
|
187
|
+
swarm attractor; and _φ<sub>i,j</sub>(t)_ and _u<sub>i,j</sub>(t+1)_ are
|
|
188
|
+
sequences of random numbers uniformly distributed on the (0,1) interval.
|
|
189
|
+
|
|
190
|
+
|
|
191
|
+
#### Example: Solving the parabola function with QPSO
|
|
192
|
+
|
|
193
|
+
Here is an example demonstrating how to find the argument that minimizes the
|
|
194
|
+
2-dimension parabola _f(x) = x<sub>1</sub><sup>2</sup> +
|
|
195
|
+
x<sub>2</sub><sup>2</sup>_ equation with PSO:
|
|
196
|
+
|
|
197
|
+
```ruby
|
|
198
|
+
require 'mhl'
|
|
199
|
+
|
|
200
|
+
solver = MHL::QuantumPSOSolver.new(
|
|
201
|
+
:swarm_size => 40, # 40 is the default swarm size
|
|
202
|
+
:constraints => {
|
|
203
|
+
:min => [ -100, -100 ],
|
|
204
|
+
:max => [ 100, 100 ],
|
|
205
|
+
},
|
|
206
|
+
:exit_condition => lambda {|iteration,best| best[:height].abs < 0.001 },
|
|
207
|
+
)
|
|
208
|
+
solver.solve(Proc.new{|x| -(x[0] ** 2 + x[1] ** 2) })
|
|
209
|
+
```
|
|
67
210
|
|
|
68
211
|
|
|
69
212
|
## License
|
|
70
213
|
|
|
71
214
|
MIT
|
|
215
|
+
|
|
216
|
+
|
|
217
|
+
## Publications
|
|
218
|
+
|
|
219
|
+
ruby-mhl was used in the following scientific publications:
|
|
220
|
+
|
|
221
|
+
[TORTONESI16] M. Tortonesi, L. Foschini, "Business-driven Service Placement for
|
|
222
|
+
Highly Dynamic and Distributed Cloud Systems", IEEE Transactions on Cloud
|
|
223
|
+
Computing, 2016 (in print).
|
|
224
|
+
|
|
225
|
+
[TORTONESI15] M.Tortonesi, "Exploring Continuous Optimization Solutions for
|
|
226
|
+
Business-driven IT Managment Problems", in Proceedings of the 14th
|
|
227
|
+
IFIP/IEEE Integrated Network Management Symposium (IM 2015) - Short papers
|
|
228
|
+
track, 11-15 May 2015, Ottawa, Canada.
|
|
229
|
+
|
|
230
|
+
[GRABARNIK14] G. Grabarnik, L. Shwartz, M. Tortonesi, "Business-Driven
|
|
231
|
+
Optimization of Component Placement for Complex Services in Federated Clouds",
|
|
232
|
+
in Proceedings of the 14th IEEE/IFIP Network Operations and Management
|
|
233
|
+
Symposium (NOMS 2014) - Mini-conference track, 5-9 May 2014, Krakow, Poland.
|
|
234
|
+
|
|
235
|
+
[FOSCHINI13] L. Foschini, M. Tortonesi, "Adaptive and Business-driven Service
|
|
236
|
+
Placement in Federated Cloud Computing Environments", in Proceedings of the 8th
|
|
237
|
+
IFIP/IEEE International Workshop on Business-driven IT Management (BDIM 2013),
|
|
238
|
+
27 May 2013, Ghent, Belgium.
|
|
239
|
+
|
|
240
|
+
If you are interested in ruby-mhl, please consider reading and citing them.
|
|
241
|
+
|
|
242
|
+
|
|
243
|
+
## References
|
|
244
|
+
|
|
245
|
+
[SUN11] Jun Sun, Choi-Hong Lai, Xiao-Jun Wu, "Particle Swarm Optimisation:
|
|
246
|
+
Classical and Quantum Perspectives", CRC Press, 2011.
|
|
247
|
+
|
|
248
|
+
[CLERC02] M. Clerc, J. Kennedy, "The particle swarm - explosion,
|
|
249
|
+
stability, and convergence in a multidimensional complex space", IEEE
|
|
250
|
+
Transactions on Evolutionary Computation, Vol. 6, No. 1, pp. 58-73,
|
|
251
|
+
2002, DOI: 10.1109/4235.985692
|
|
252
|
+
|
|
253
|
+
[BLACKWELL04] Tim Blackwell, Jürgen Branke, "Multi-swarm Optimization in
|
|
254
|
+
Dynamic Environments", Applications of Evolutionary Computing, pp. 489-500,
|
|
255
|
+
Springer, 2004. DOI: 10.1007/978-3-540-24653-4\_50
|
|
256
|
+
|
|
257
|
+
[REZAEEJORDEHI13] A. Rezaee Jordehi, J. Jasni, "Parameter selection in particle
|
|
258
|
+
swarm optimisation: a survey", Journal of Experimental & Theoretical Artificial
|
|
259
|
+
Intelligence, Vol. 25, No. 4, pp. 527-542, 2013. DOI: 10.1080/0952813X.2013.782348
|
|
260
|
+
|
|
261
|
+
[CLERC12] M. Clerc, "Standard Particle Swarm Optimisation - From 2006 to 2011",
|
|
262
|
+
available at: [http://clerc.maurice.free.fr/pso/SPSO\_descriptions.pdf](http://clerc.maurice.free.fr/pso/SPSO_descriptions.pdf)
|
data/lib/mhl/charged_swarm.rb
CHANGED
|
@@ -1,5 +1,3 @@
|
|
|
1
|
-
require 'matrix'
|
|
2
|
-
|
|
3
1
|
require 'mhl/generic_swarm'
|
|
4
2
|
|
|
5
3
|
|
|
@@ -13,7 +11,7 @@ module MHL
|
|
|
13
11
|
def initialize(size, initial_positions, initial_velocities, params={})
|
|
14
12
|
@size = size
|
|
15
13
|
|
|
16
|
-
# retrieve ratio between charged (QPSO) and neutral (PSO
|
|
14
|
+
# retrieve ratio between charged (QPSO) and neutral (constrained PSO) particles
|
|
17
15
|
ratio = (params[:charged_to_neutral_ratio] || DEFAULT_CHARGED_TO_NEUTRAL_RATIO).to_f
|
|
18
16
|
unless ratio > 0.0
|
|
19
17
|
raise ArgumentError, 'Parameter :charged_to_neutral_ratio should be a real greater than zero!'
|
|
@@ -35,51 +33,65 @@ module MHL
|
|
|
35
33
|
# find problem dimension
|
|
36
34
|
@dimension = initial_positions[0].size
|
|
37
35
|
|
|
38
|
-
@
|
|
36
|
+
@iteration = 1
|
|
39
37
|
|
|
40
38
|
# define procedure to get dynamic value for alpha
|
|
41
39
|
@get_alpha = if params.has_key? :alpha and params[:alpha].respond_to? :call
|
|
42
40
|
params[:alpha]
|
|
43
41
|
else
|
|
44
|
-
->(
|
|
42
|
+
->(it) { (params[:alpha] || DEFAULT_ALPHA).to_f }
|
|
45
43
|
end
|
|
46
44
|
|
|
47
45
|
# get values for parameters C1 and C2
|
|
48
46
|
@c1 = (params[:c1] || DEFAULT_C1).to_f
|
|
49
47
|
@c2 = (params[:c1] || DEFAULT_C2).to_f
|
|
50
48
|
|
|
51
|
-
# define procedure to get dynamic value for
|
|
52
|
-
@
|
|
53
|
-
params[:
|
|
49
|
+
# define procedure to get dynamic value for chi
|
|
50
|
+
@get_chi = if params.has_key? :chi and params[:chi].respond_to? :call
|
|
51
|
+
params[:chi]
|
|
54
52
|
else
|
|
55
|
-
->(
|
|
53
|
+
->(it) { (params[:chi] || DEFAULT_CHI).to_f }
|
|
54
|
+
end
|
|
55
|
+
|
|
56
|
+
if params.has_key? :constraints
|
|
57
|
+
puts "ChargedSwarm called w/ constraints: #{params[:constraints]}"
|
|
56
58
|
end
|
|
59
|
+
|
|
60
|
+
@constraints = params[:constraints]
|
|
57
61
|
end
|
|
58
62
|
|
|
59
63
|
def mutate
|
|
60
64
|
# get alpha parameter
|
|
61
|
-
alpha = @get_alpha.call(@
|
|
65
|
+
alpha = @get_alpha.call(@iteration)
|
|
62
66
|
|
|
63
|
-
# get
|
|
64
|
-
|
|
67
|
+
# get chi parameter
|
|
68
|
+
chi = @get_chi.call(@iteration)
|
|
65
69
|
|
|
66
|
-
# this calculates the C_n parameter (
|
|
67
|
-
# attractors) as defined in
|
|
70
|
+
# this calculates the C_n parameter (the centroid of the set of all the
|
|
71
|
+
# particle attractors) as defined in equations 4.81 and 4.82 of [SUN11].
|
|
68
72
|
#
|
|
69
|
-
#
|
|
70
|
-
#
|
|
71
|
-
|
|
73
|
+
# Note: we consider ALL the particles here, not just the charged (QPSO)
|
|
74
|
+
# ones. As a result, the neutral particles influence the behavior of the
|
|
75
|
+
# charged ones not only by defining the swarm attractor, but also the
|
|
76
|
+
# centroid.
|
|
77
|
+
attractors = @particles.map {|p| p.attractor[:position] }
|
|
78
|
+
c_n = 0.upto(@dimension-1).map do |j|
|
|
79
|
+
attractors.inject(0.0) {|s,attr| s += attr[j] } / @size.to_f
|
|
80
|
+
end
|
|
72
81
|
|
|
73
82
|
@particles.each_with_index do |p,i|
|
|
74
83
|
# remember: the particles are kept in a PSO-first and QPSO-last order
|
|
75
84
|
if i < @num_neutral_particles
|
|
76
|
-
p.move(
|
|
85
|
+
p.move(chi, @c1, @c2, @swarm_attractor)
|
|
77
86
|
else
|
|
78
87
|
p.move(alpha, c_n, @swarm_attractor)
|
|
79
88
|
end
|
|
89
|
+
if @constraints
|
|
90
|
+
p.remain_within(@constraints)
|
|
91
|
+
end
|
|
80
92
|
end
|
|
81
93
|
|
|
82
|
-
@
|
|
94
|
+
@iteration += 1
|
|
83
95
|
end
|
|
84
96
|
end
|
|
85
97
|
end
|
data/lib/mhl/generic_particle.rb
CHANGED
|
@@ -19,34 +19,6 @@ module MHL
|
|
|
19
19
|
end
|
|
20
20
|
end
|
|
21
21
|
|
|
22
|
-
def remain_within(constraints)
|
|
23
|
-
new_pos = @position.map.with_index do |x,i|
|
|
24
|
-
puts "resetting #{x} within #{constraints[:min][i]} and #{constraints[:max][i]}"
|
|
25
|
-
d_max = constraints[:max][i]
|
|
26
|
-
d_min = constraints[:min][i]
|
|
27
|
-
d_size = d_max - d_min
|
|
28
|
-
if x > d_max
|
|
29
|
-
while x > d_max + d_size
|
|
30
|
-
x -= d_size
|
|
31
|
-
end
|
|
32
|
-
if x > d_max
|
|
33
|
-
x = 2 * d_max - x
|
|
34
|
-
end
|
|
35
|
-
elsif x < d_min
|
|
36
|
-
while x < d_min - d_size
|
|
37
|
-
x += d_size
|
|
38
|
-
end
|
|
39
|
-
if x < d_min
|
|
40
|
-
x = 2 * d_min - x
|
|
41
|
-
end
|
|
42
|
-
end
|
|
43
|
-
puts "now x is #{x}"
|
|
44
|
-
x
|
|
45
|
-
end
|
|
46
|
-
puts "new_pos: #{new_pos}"
|
|
47
|
-
@position = new_pos # Vector[new_pos]
|
|
48
|
-
end
|
|
49
|
-
|
|
50
22
|
end
|
|
51
23
|
|
|
52
24
|
end
|
data/lib/mhl/generic_swarm.rb
CHANGED
|
@@ -3,20 +3,22 @@ require 'forwardable'
|
|
|
3
3
|
module MHL
|
|
4
4
|
class GenericSwarmBehavior
|
|
5
5
|
|
|
6
|
-
# The following values
|
|
7
|
-
#
|
|
8
|
-
# Applications of Evolutionary Computing, pp. 489-500, Springer, 2004.
|
|
9
|
-
# DOI: 10.1007/978-3-540-24653-4_50
|
|
6
|
+
# The following values are considered a best practice [SUN11] [CLERC02]
|
|
7
|
+
# [BLACKWELLBRANKE04].
|
|
10
8
|
# C_1 is the cognitive acceleration coefficient
|
|
11
9
|
DEFAULT_C1 = 2.05
|
|
12
10
|
# C_2 is the social acceleration coefficient
|
|
13
11
|
DEFAULT_C2 = 2.05
|
|
12
|
+
# \chi is the constraining factor for normal particles
|
|
14
13
|
PHI = DEFAULT_C1 + DEFAULT_C2
|
|
15
|
-
|
|
16
|
-
|
|
17
|
-
|
|
18
|
-
#
|
|
19
|
-
#
|
|
14
|
+
DEFAULT_CHI = 2.0 / (2 - PHI - Math.sqrt((PHI ** 2 - 4.0 * PHI))).abs
|
|
15
|
+
|
|
16
|
+
# \alpha is the contraction-expansion (CE) coefficient for quantum
|
|
17
|
+
# particles [SUN11].
|
|
18
|
+
# In order for the QPSO algorithm to converge, \alpha must be lower than
|
|
19
|
+
# $e^{\gamma} \approx 1.781$, where $\gamma \approx 0.5772156649$ is the
|
|
20
|
+
# Euler constant. According to [SUN11], 0.75 looks like a sensible default
|
|
21
|
+
# parameter.
|
|
20
22
|
DEFAULT_ALPHA = 0.75
|
|
21
23
|
|
|
22
24
|
extend Forwardable
|
|
@@ -29,7 +31,7 @@ module MHL
|
|
|
29
31
|
particle_attractors = @particles.map { |p| p.attractor }
|
|
30
32
|
|
|
31
33
|
# update swarm attractor (if needed)
|
|
32
|
-
|
|
34
|
+
unless (defined?(@swarm_attractor))
|
|
33
35
|
@swarm_attractor = particle_attractors.max_by {|p| p[:height] }
|
|
34
36
|
else
|
|
35
37
|
@swarm_attractor = [ @swarm_attractor, *particle_attractors ].max_by {|p| p[:height] }
|